شما در حال خواندن درس تعیین استقرار با منحنی محصول-مقدار و منحنی هزینه-مقدار هستید. این درس مربوط به مجموعه طرحریزی است.
در درسهای گذشته با انواع استقرار محصولی، فرایندی، ثابت و ترکیبی (مثل چیدمانی که با تکنولوژی گروهی تعیین میشود) آشنا شدید. در یک کارخانه ممکن است مجموعهای از این چیدمانها مورد استفاده قرار بگیرد، مثلاً برای تولید یک قطعه خاص از خط تولید -استقرار محصولی- و برای ساخت سایر قطعات از یک کارگاه عمومی -استقرار فرایندی- استفاده شود. همچنین شاید در بخشی از کارخانه، واحدی به صورت مکان ثابت طرحریزی شده باشد تا برای انجام کارهای پژوهشی مورد استفاده قرار بگیرد. بنابراین در واحد تولیدی، ممکن است برای تولید هر قطعه یا محصول از بخشهایی با چیدمان متقاوت استفاده شود. در این میان، چالش مهم این است که: برای تولید هر قطعه، استفاده از کدام روش استقرار مناسب است؟
برای این سؤال، پاسخ واحد و مشخصی وجود ندارد و حسب مورد میتوان از معیارها و روشهای متفاوتی استفاده کرد. اما از میان این روشها و معیارها، در این درس با دو روش تحلیل با نمودار محصول-مقدار (P-Q) و تحلیل با نقطهی سربهسر یا نمودار هزینه-مقدار (C-Q) آشنا خواهید شد. لازم به ذکر است که در بسیاری از منابع طرحریزی به این روشها اشاره شده و استفاده از آنها رایج است.
تعیین استقرار با نمودار محصول-مقدار
دو پارامتر مهمی که میتوانند مبنای انتخاب بهترین روش استقرار باشند: «تنوع محصولات» و «ظرفیت تولید محصولات» هستند. به عنوان مثال، اگر بخواهیم محصولی را در ظرفیت بسیار بالا تولید کنیم، استقرار محصولی بهترین گزینه است و امکان استفاده از استقرار فرایندی یا استقرار مکان ثابت وجود ندارد. اگر بخواهیم چندین قطعهی مختلف اما مشابه را در ظرفیت اندک تولید کنیم، استقرار محصولی توجیهپذیر نیست و استقرارهای فرایندی و ترکیبی مناسبتر به نظر میرسند.
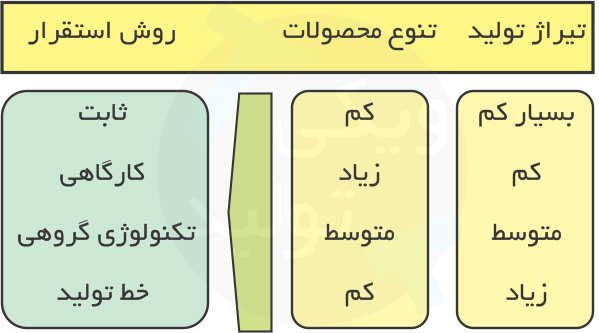
در نمودار محصول-مقدار (Product-Quantity)، «انواع قطعات» روی محور افقی و «مقدار هر قطعه» روی محور عمودی درج میشود. به عنوان مثال اگر بخواهیم دو قطعهی الف و ب را بسازیم و از اتصال آنها با بکدیگر، قطعهی ج را تولید کنیم، محور افقی نمودارمان شامل «قطعه الف»، «قطعه ب» و «قطعه ج» میشود. همچنین در این نمودار، قطعات به ترتیب مقدارشان از چپ به راست مرتب میشوند؛ مثلاً اگر ظرفیت تولید قطعهی ب ۱۰۰۰ واحد و ظرفیت تولید قطعهی الف ۵۰۰ واحد باشد، ابتدا قطعهی ب و سپس قطعهی الف را درج میکنیم. بدیهی است هر چه تعداد قطعات بیشتر باشد، به معنای تنوع بالاتر است؛ بنابراین در این نمودار به هر دو پارامتر «تنوع محصولات» و «ظرفیت تولید محصولات» دسترسی داریم.

در مورد درج محصولات روی محور افقی، گاهاً تصور میشود که اگر اسامی قطعات سازندهی یک محصول درج شده باشد، نیازی به درج محصول نهایی نیست؛ مثلاً چون قطعهی ۳ از مونتاژ قطعات ۱ و ۲ به وجود میآید و اسم این دو قطعه درج شده است، لازم نیست اسم قطعهی ۳ روی محور افقی درج شود. این برداشت لزوماً درست نیست، زیرا شاید تولید قطعهی ۳ (یا مونتاژ قطعات ۱ و ۲) نسبت به تولید قطعات ۱ و ۲ به چیدمان متفاوتی نیاز داشته باشد. به عنوان مثال، بازوی جرثقیل از اتصال دهها قطعهی کوچکتر فلزی تولید میشود، حال آن که این قطعات فلزی احتمالاً خروجی استقرار محصولی -یا شاید فرایندی- هستند، اما بازوی جرثقیل احتمالاً در محیطی با چیدمان مکان ثابت مونتاژ میشود.
نباید فراموش کنیم که منحنی محصول-مقدار صرفاً یک ابزار است و متناسب با اهدافمان، میتوانیم به روشهای مختلفی از آن استفاده کنیم. به عنوان مثال، گاهاً این سؤال مطرح میشود که: آیا باید همهی قطعات را در نمودار فهرست کنیم؟ حال آن که پاسخ دقیقی برای این سؤال وجود ندارد و باید شرایط مسأله را لحاظ کنیم. مثلاً اگر از قبل تکلیف بعضی قطعات روشن است و در مورد آنها تصمیمگیری شده، میتوانیم از درج اسامی آنها خودداری کنیم. همچنین شاید مناسبتر باشد که محصولات را در قالب چند نمودار مختلف -به جای یک نمودار- نشان دهیم؛ مثلاً اگر کارخانهای داریم که در آن «چند نوع کپسول فلزی» و «چند نوع گاز مختلف» تولید میشود، مناسبتر است که انواع کپسولها را در یک نمودار و انواع گازها را در نموداری دیگر نشان دهیم. در غیر این صورت، عملاً امکان مقایسهی «۲۰ عدد کپسول گاز» یا «۲۰۰۰ لیتر گاز هلیوم» بوجود ندارد. ضمن این که میدانیم «محل تولید کپسولها» و «محل تولید فراوردههای گازی» مستقل و جدا از یکدیگر هستند و درج آنها در یک نمودار بیفایده است.
اگر نمودار محصول-مقدار مثل تصویر زیر عمیق باشد، معمولاً مجبوریم برای تولید محصولات مورد نظر از چند نوع استقرار مختلف استفاد کنیم، مثلاً بعضی از آنها را با خط تولید و بعضی دیگر را در یک چیدمان کارگاهی بسازیم.

با توجه به نمودار بالا، محصولات را میتوانیم به سه گروه زیر تقسیم کنیم:
گروه اول شامل سه قطعه (تنوع کم) با مقدار تولید زیاد است که هماهنگی بیشتری با استقرار محصولی دارند.
گروه دوم شامل نه قطعه (تنوع متوسط) با مقدار تولید متوسط است که احتمالاً هماهنگی بیشتری با استقرار گروهی دارند. همچنین شاید بتوانیم از «استقرار محصولی با سطح بالاتری از انعطافپذیری» یا از «استقرار فرایندی با سطح بالاتری از سفارشیسازی» استفاده کنیم.
گروه سوم شامل تعداد زیادی قطعه (تنوع زیاد) با مقدار اندک است که احتمالاً هماهنگی بیشتری با استقرار فرایندی دارند.
ضمناً از میان قطعاتی که در مقدار کم تولید میشوند، اگر جابهجایی آنها دشوار باشد یا سایر شرایط مندرج در این درس وجود داشته باشد، میتوانیم از استقرار ثابت استفاده کنیم.
اگر عمق منحنی مثل تصویر زیر کم باشد، امکان استفاده از «یک نوع خاص از استقرار» افزایش مییابد. مثلاً در نمودار زیر، تنوع محصولات کم و مقدارشان زیاد است، بنابراین میتوانیم برای همهی آنها از استقرار محصولی استفاده کنیم.

در نمودار زیر تنوع محصولات زیاد و مقدار تولیدشان اندک است، پس به نظر میرسد استقرار فرایندی گزینهی مناسبتری برای تولیدشان باشد. همچنین شاید تصمیم بگیریم که بخشی از قطعات، مثلاً قطعات یک تا پانزده با استقرار گروهی و سایر قطعات با استقرار فرایندی تولید شوند.

تعیین استقرار با منحنی هزینه-مقدار
منحنی هزینه-مقدار، کاربرد زیادی در تصمیمهای مهندسی دارد و در بحث تعیین استقرار نیز مفید است. در این منحنی، تغییرات «هزینهی تولید» نسبت به «مقدار تولید» نشان داده میشود. برای تعیین استقرار، میتوانیم نمودار هزینه-مقدار را برای هر یک از روشهای استقرار (فرایندی، محصولی، ثابت، گروهی) ترسیم کنیم و ببینیم برای تولید هر محصول در ازای مقادیر مختلف، کدام استقرار ارزانتر تمام میشود. نتیجهی نهایی میتواند شبیه فهرست زیر باشد:
اگر میخواهیم الف را کمتر از ۱۰۰ عدد در ماه تولید کنیم، هزینههای ناشی از استقرار کارگاهی کمتر است.
اگر میخواهیم الف را بیش از ۱۰۰ عدد و کمتر از ۱۰۰۰ عدد در ماه تولید کنیم، هزینههای ناشی استقرار گروهی کمتر است.
اگر میخواهیم الف را بیش از ۱۰۰۰ عدد در ماه تولید کنیم، هزینههای ناشی از استقرار محصولی کمتر است.
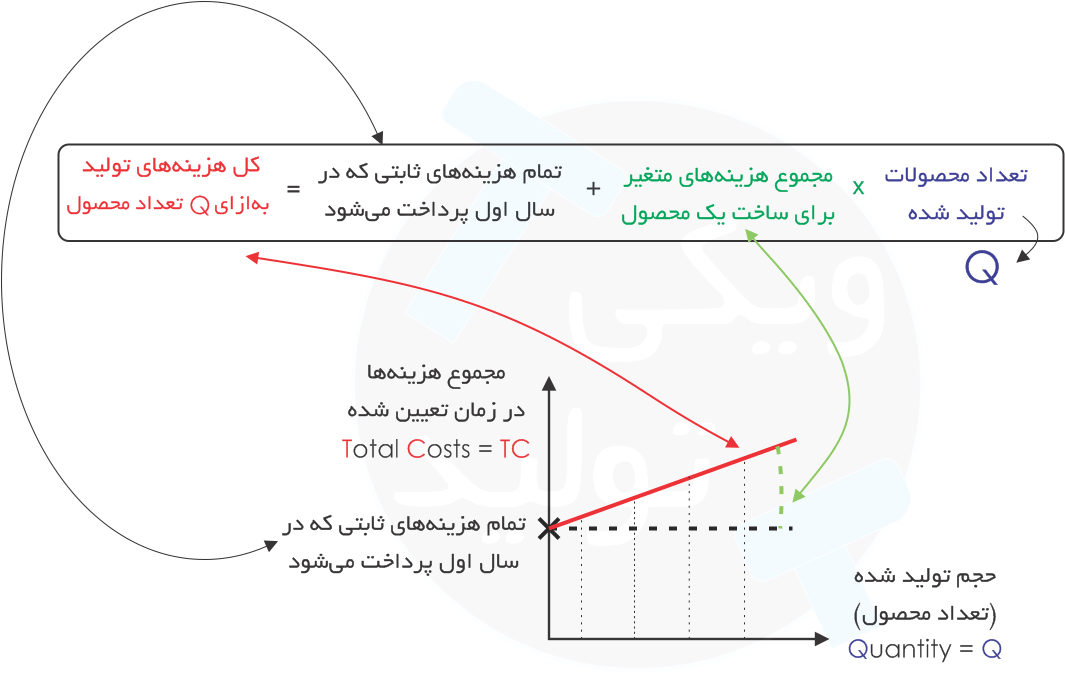
در تصویر زیر، محور افقی نمودار «مقدار تولید» محصول و محور عمودی «هزینه تولید» را نشان میدهد. همانطور که میبینید، اگر بخواهیم محصول مورد نظرمان را به تعداد Q واحد تولید کنیم، مجموع هزینههای آن TC1 میشود.

در درس هزینههای ثابت و متغیر توضیح دادیم که هزینهها را میتوان به ثابت (Fixed) و متغیر (Variable) تقسیم کرد و مجموع آنها، هزینهی کل را نشان میدهد:

مجموع هزینههای متغیر را میتوان از رابطهی زیر محابسه کرد:

در مورد هزینههای ثابت، «بازهی زمانی مورد نظر» تأثیر بسیار زیادی دارد. به عنوان مثال، ممکن است از قبل سولهای برای واحد تولیدی خریداری شده باشد و وقتی بازهی زمانی «دو ماه آینده» تا «شش ماه آینده» را در نظر میگیریم، این هزینه لحاظ نشود. اما به صورت کلّی چون موضوع صحبتمان تعیین استقرار است و عموماً هزینههای سرمایهگذاری -همچون خرید زمین و احداث ساختمانها و سولهها- در تصمیمهایمان مؤثر است، معمولاً چنین هزینههایی را نیز لحاظ میکنیم. به عبارت دیگر، بازهی زمانی را طوری انتخاب میکنیم که در بردارندهی چنین هزینههایی باشد.
در تصویر زیر، بازهی زمانی مورد نظرمان را «اولین سال فعالیت کارخانه» در نظر گرفتیم و «هزینهی تولید محصول» در ازای «مقادیر مختلف» را نشان دادهیم. خط قرمز منحنی هزینه-مقدار است. بدیهی است که اگر در سال اول هیچ محصولی تولید نشود، مجموع هزینهها برابر با «مجموع هزینههای ثابت در سال اول» خواهد بود. با افزایش مقدار تولید، هزینههای متغیر نیز به هزینههای ثابت اضافه میشوند و مجموع هزینه را افزایش میدهند.
اگر هزینههای تولید محصول با استقرار محصولی، استقرار فرایندی، استقرار مکان ثابت و استقرار گروهی را رسم کنیم، نموداری شبیه زیر تشکیل میشود. همانطور که در مثال بالا میبینید، هزینهی ثابت برای «استقرار ثابت» کمتر و هزینهی ثابت برای «استقرار محصولی» بیشتر از سایر روشهای استقرار است. این موضوع را جنین میتوان توجیه کرد که اصولاً تهیهی خط تولید و تجهیزات سفارشی پرهزینه و زمانبر است.

ناظر بر نمودار بالا، اگر قرار باشد محصول را کمتر از مقدار Q1 تولید کنیم، هزینههای ناشی از استقرار ثابت کمتر است. اما اگر مقدار تولید از Q1 تا Q2 باشد، استقرار کارگاهی به صرفهتر است. برای تولید از مقدار Q2 تا Q3، هزینههای ناشی از استقرار با روش تکنولوژی گروهی کمتر است و برای تولید محصول در مقداری بیش از Q3، استقرار محصولی ارزانتر تمام میشود. البته لازم به ذکر است که «بازهی زمانی مورد نظر» تأثیر زیادی در شکل نمودارها دارد و با تغییر آن، مقادیر Q تغییر میکنند.
Q1 محل تلاقی منحنی دو منحنی مربوط به «استقرار محل ثابت» و «استقرار کارگاهی» است و مقدار آن را میتوانیم از رابطهی زیر حساب کنیم. ضمناً مقادیر Q2 و Q3 را نیز میتوانیم به همین روش محاسبه کنیم.


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.