شما در حال خواندن درس نمو هموار برای پیشبینی سریهای زمانی از مجموعه پیشبینی تقاضا هستید.
روش هموارسازی نمایی (Exponential Smoothing) یا نمو هموار برای پیشبینی سریهای زمانی است. این روش از دادههای گذشته برای پیشبینی آینده استفاده میکند، اما همه دادههای را با وزن یکسان در نظر نمیگیرد؛ بلکه دادههای اخیر را مهمتر از دادههای قدیمی قلمداد میکند.
روش هموارسازی نمایی، اشکال مختلفی دارد. در این درس روش هموارسازی نمایی ساده و روش هموارسازی نمایی دوبل را بررسی خواهیم کرد.
هموارسازی ساده نمیتواند روند افزایش یا کاهشی و تغییرات فصلی دادهها را تصحیح کند؛ بنابراین برای دادههای مبتنی بر الگوی روند (Trend) و الگوی فصلی (Seosonal) مناسب نیست.
روش هموارسازی دوبل یا هولت مشابه هموارسازی ساده است، با این تفاوت که میتواند روند افزایشی یا کاهشی دادهها را جبران کند. بنابراین میتوانیم از آن برای پیشبینی دادههای مبتنی بر الگوی روند استفاده کنیم.
روش دیگری به اسم هموارسازی سهگانه یا وینتر وجود دارد که میتواند علاوه بر جبران روند کاهشی یا افزایشی، تغییرات فصلی را نیز لحاظ کند. بنابراین میتوانیم از آن برای پیشبینی دادههای مبتنی بر الگوی روند و الگوی فصلی استفاده کنیم. اما در این درس، روش وینتر را بررسی نخواهیم کرد.
هموارسازی نمایی ساده
فرض کنید میخواهیم از روش هموارسازی نمایی ساده برای پیشبینی مقدار فروش استفاده کنیم. برای این روش به سه مقدار نیاز داریم:
مقدار اول، مقدار واقعی فروش در آخرین دوره است. مثلاً برای پیشبینی فروش در دورهی دهم، باید مقدار واقعی فروش در دوره نهم را بدانیم. اگر واحد زمان ماه باشد، برای پیشبینی فروش در ماه اسفند، باید مقدار واقعی فروش در ماه بهمن را بدانیم. اگر واحد زمان سال باشد، برای پیشبینی فروش در سال ۲۰۲۵ باید مقدار واقعی تقاضا در سال ۲۰۲۴ را بدانیم.
مقدار دوم، فروش پیشبینی شده برای آخرین دوره است. مثلاً فرض کنید فروش واقعی در دوره نهم ۱۰۰۰ واحد بوده باشد؛ این مقدار اول است که بالاتر گفتیم. اما شاید پیشبینی ما برای دوره نهم این بوده باشد که فروش به ۸۰۰ واحد میرسد. عدد ۸۰۰ نیز دومین مقداری است که نیاز داریم.
مقدار سوم، ضریب آلفا است. برای پیشبینی با نمو هموار ساده، فرض میکنیم فروش در دوره بعدی، برابر است با: میانگین وزندار فروش آخرین دوره (مقدار اول) و فروش پیشبینی شده برای آخرین دوره (مقدار دوم). میانگین وزندار یعنی به هر کدام از این دو پارامتر ضریب دهیم تا به همان نسبت در میانگین مؤثر باشند. معدل دانشآموزان نیز به همین شکل حساب میشود، یعنی هر درس ضریبی دارد و تاثیر همهی آنها در میانگین برابر نیست. آلفا ضریبی است که به مقدار واقعی فروش در آخرین دوره میدهیم. این عدد باید بین صفر و یک باشد. اگر آلفا را ۰.۴ انتخاب کنیم، به این معنا است که مقدار واقعی فروش در آخرین دوره به اندازه ۴۰٪ و مقدار پیشبینی شده برای آن دوره به اندازه ۶۰٪ بر میانگین نهایی اثر میگذارد.
با توجه به توضیحاتی که دادیم، مقداری که برای فروش در دورهی جدید -یک دوره بعد از آخرین دوره- پیشبینی میکنیم با رابطه زیر به دست میآید. در این رابطه Ft+1 مقدار فروشی است که میخواهیم پیشبینی کنیم. At مقدار واقعی فروش در آخرین دوره و Ft مقدار فروش پیشبینی شده برای آخرین دوره است.

رابطهی بالا را میتوانیم به شکل زیر هم بنویسیم.
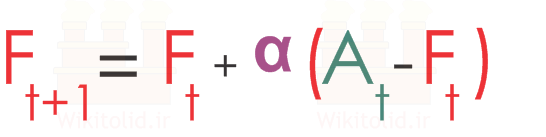
در ادامه چگونگی استفاده از روش هموارسازی نمایی ساده را با مثال توضیح خواهیم داد. در جدول زیر، تعداد فروش در هر ماه ثبت شده است. میخواهیم بر اساس این اطلاعات، از روش نمو هموار برای پیشبینی فروش در ماه سیزدهم استفاده کنیم.
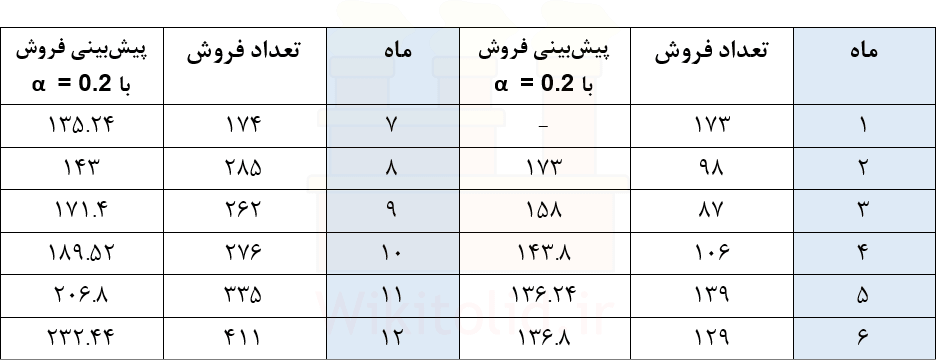
برای پیشبینی فروش ابتدا باید مقدار آلفا را حساب کنیم. برای شناسایی مناسبترین مقدار برای آلفا، میتوانیم پیشبینی را با مقادیر مختلف آن انجام دهیم و بررسی کنیم که خطای پیشبینی در ازای کدام آلفا کمتر است. نرمافزارهای آماری خودشان این کار را انجام، و بهترین مقدار آلفا را پیشنهاد میدهند. در این مثال برای شروع، آلفا را ۰.۲ فرض میکنیم.
برای پیشبینی مقدار فروش در دوره سیزدهم، باید مقدار واقعی فروش در دوره دوازدهم را بدانیم. این مقدار در جدول موجود است. همچنین باید مقدار تقاضای پیشبینی شده برای دوره دوازهم را بدانیم. برای این کار، مقدار تقاضا در همه دورهها -از دوره یک تا دوازده- را پیشبینی میکنیم تا به دوره دوازده برسیم. هدف این است که ببینیم اگر فروش در هر دوره را با آلفای ۰.۲ پیشبینی کنیم، چه مقداری به دست میآید و چقدر با مقدار واقعی تفاوت دارد.
برای دوره اول نمیتوانیم مقدار فروش را پیشبینی کنیم. چون گفتیم برای پیشبینی مقدار فروش در هر دوره به سه مقدار «آلفا»، «فروش در آخرین دوره» و «فروش پیشبینی شده برای آخرید دوره» نیاز داریم. اما اکنون در مورد دورهی قبلی، هیچ اطلاعی نداریم.
برای ماه دوم، «آخرین فروش در دوره اول» برابر ۱۷۳ است. اما «مقدار فروش پیشبینی شده برای دوره اول» وجود ندارد، چون برای دور اول به اطلاعات کافی برای پیشبینی دسترسی نداشتیم. در این مرحله از روش نایو استفاده میکنیم و تقاضا برای ماه دوم را ۱۷۳ واحد در نظر میگیریم. مطابق روش نایو، مقدار فروش هر دوره برابر با مقدار فروش در آخرین دوره است.
برای پیشبینی تقاضا در ماه سوم، میدانیم تقاضای واقعی در ماه دوم ۱۷۳ واحد بوده و همچنین تقاضا در آن دوره را نیز ۱۷۳ واحد پیشبینی کردیم. آلفا ۰.۲ است. میانگین وزندار میگیریم و مطابق رابطهای که بالاتر نوشتیم، مقدار فروش برای ماه سوم را ۱۵۸ واحد پیشبینی میکنیم.
به ترتیب مقدار فروش برای ماههای چهارم تا دوازدهم را پیشبینی میکنیم. با پیدا کردن مقدار پیشبینی شده برای دوره دوازدهم، به سادگی میتوانیم مقدار تقاضا برای دوره سیزدهم را نیز پیشبینی کنیم.
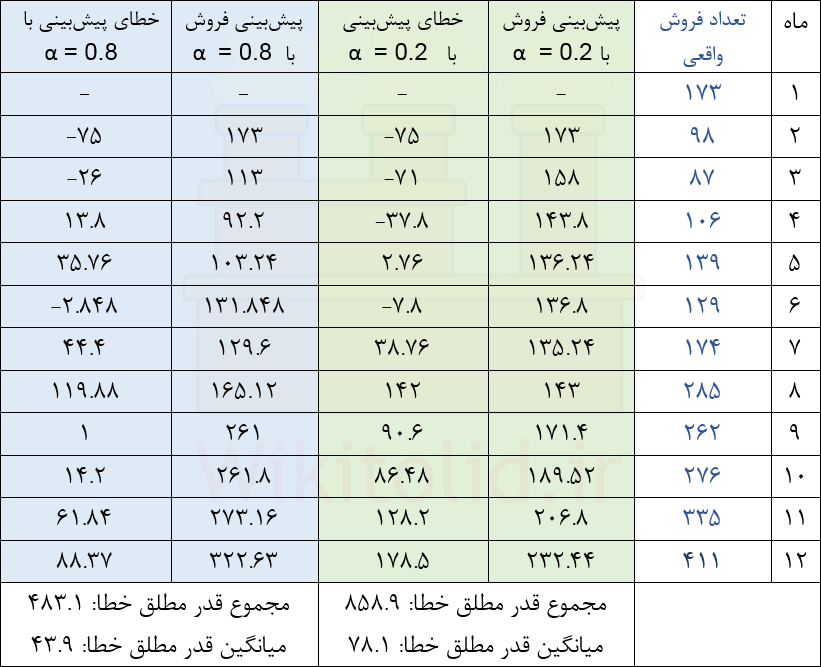
گفتیم برای پیدا کردن مقدار مناسب آلفا باید آزمون وخطا کنیم. پس مناسب است که پیشبینی را بر اساس مقادیر دیگر آلفا انجام دهیم و نتایج را مقایسه کنیم. در این مثال، محاسبات را با آلفای ۰.۸ تکرار کردیم. میانگین خطای پیشبینی با آلفای ۰.۸ کمتر از آلفای ۰.۲ است. برای همین، آلفای ۰.۸ گزینه مناسبتری به نظر میرسد.
استفاده از روش هموارسازی نمایی ساده در اکسل
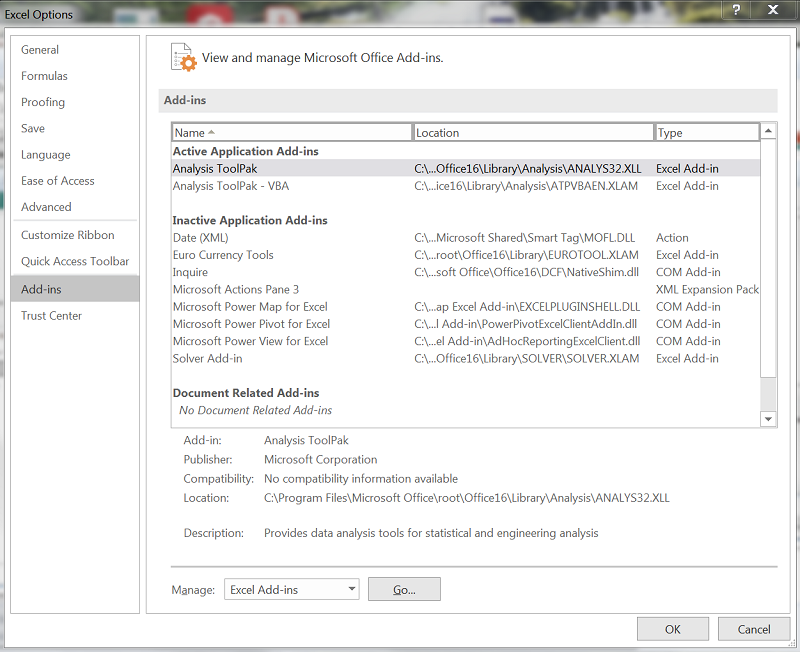
برای استفاده از این روش در اکسل، ابتدا باید ابزارهای تحلیل داده را فعال کنیم. برای این کار از منوی File به Options میرویم و روی Add-ins کلیک میکنیم. در Manage، گزینهی Excel Add-ins را انتخاب میکنیم و Go را میزنیم.
گزینهی Analysis Toolpak را فعال میکنیم.
در اکسل، اطلاعات مربوط به فروش را در یک ستون ثبت میکنیم. سپس از منوی DATA روی DATA Analysis کلیک کرده و Exponential Smoothing را انتخاب میکنیم.
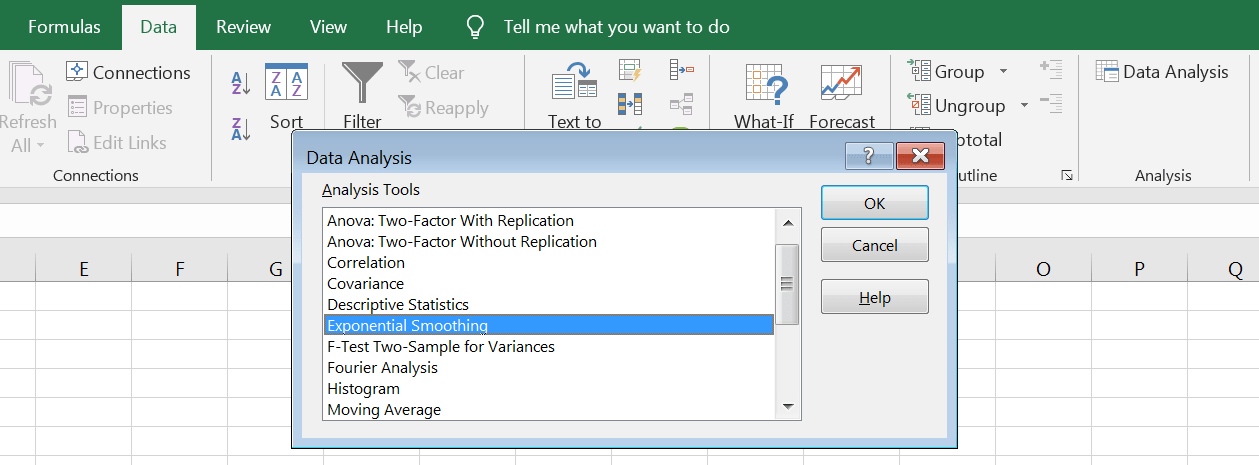
برای Input Range مقادیری که ثبت کردهایم را به اضافه یک سلول اضافه -یک سلول خالی در پایین آخرین مقدار- انتخاب میکنیم. اگر خانه خالی را انتخاب نکنیم، دوره بعدی پیشبینی نخواهد شد.
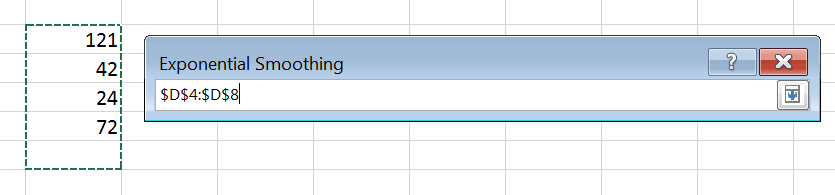
در Output Range مشخص میکنیم که جوابها در کدام سلول مشخص شوند. یک سلول را انتخاب میکنیم. مقدار Damping Factor تفاضل مقدار آلفا از عدد یک را نشان میدهد، یعنی برای آلفای ۰٫۴ مقدار Damping Factor را ۰٫۶ انتخاب میکنیم. تایید را میزنیم تا محاسبات انجام شود.
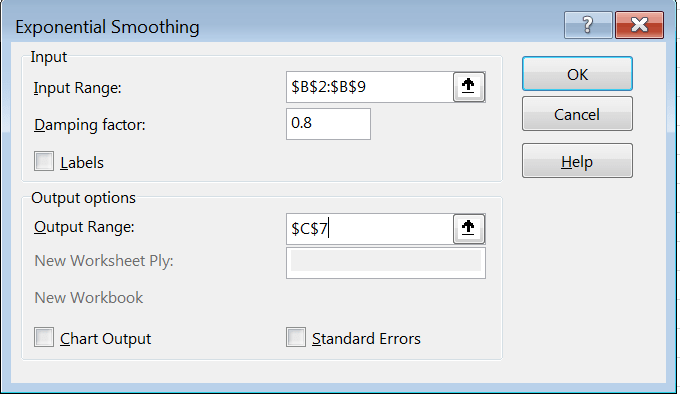
اگر تیک Labels فعال باشد، اولین مقدار وارد شده به عنوان اسم ستون در نظر گرفته میشود و در محاسبات لحاظ نمیشود. بنابراین اگر بالای ستونی که اطلاعات در آن درج شده، عنوانی مثل «میزان فروش» نوشتهایم، تیک را میزنیم. اما اگر عنوانی درج نشده و از ابتدا اعداد را وارد کردهایم، تیک را بر میداریم.
روش هموارسازی نمایی با تصحیح روند
گاهی اوقات سریهای زمانی از الگوی روند (Trend) پیروی میکنند و مقادیر آنها به طور مداوم افزایش یا کاهش مییابد. هموارسازی نمایی ساده نمیتواند روند افزایشی یا کاهش این دادهها را جبران کند. اما هموارسازی نمایی دوبل، میتواند تغییرات تقاضا به دلیل روند افزایشی یا کاهشی دادهها را هم در نظر بگیرد. این روش به شکل زیر است:

در رابطه بالا، Ft+1 همان رابطهای است که در بخش اول درس بررسی کردیم؛ یعنی مقدار پیشبینی شده برای تقاضا با روش نمو هموار ساده است. یادآوری میکنیم که نمو هموار ساده از رابطه زیر به دست میآید:
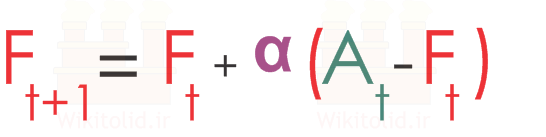
جملهی دوم یا Tt+1 مقداری است که برای جبران افزایش یا کاهش ناشی از الگوی روند به نتیجه پیشبینی اضافه میشود. این مقدار را هم با روش نمو هموار ساده محاسبه میکنیم. به عبارتی: ابتدا تقاضا را با نمو هموار ساده پیشبینی میکنیم. سپس تغییرات مرتبط با روند افزایشی یا کاهشی دادهها را نیز با نمو هموار ساده پیشبینی میکنیم. مجموع این مقادیر، پیشبینی نهایی ما از فروش است.
رابطه زیر، بخش دوم رابطهای است که بالاتر نوشتیم. همانطور که گفتیم این رابطه هم بر اساس نمو هموار ساده است. فقط جای آلفا، باید ضریب دیگری به اسم بتا تعریف کنیم.

در ادامه، مثالی که بالاتر با نمو هموار ساده حل کردیم، با روش هموارسازی نمایی دوبل حل میکنیم. در بخش قبل گفتیم که ۰.۸ برای آلفا مناسبتر از ۰.۲ است. برای تعیین مقدار بتا نیز میتوانیم آزمون و خطا کنیم. اما چون جدولمان جا ندارد و روش آزمون و خطا را بالاتر گفتیم، فرض میکنیم مقدار ۰.۵ برای بتا مناسب است.
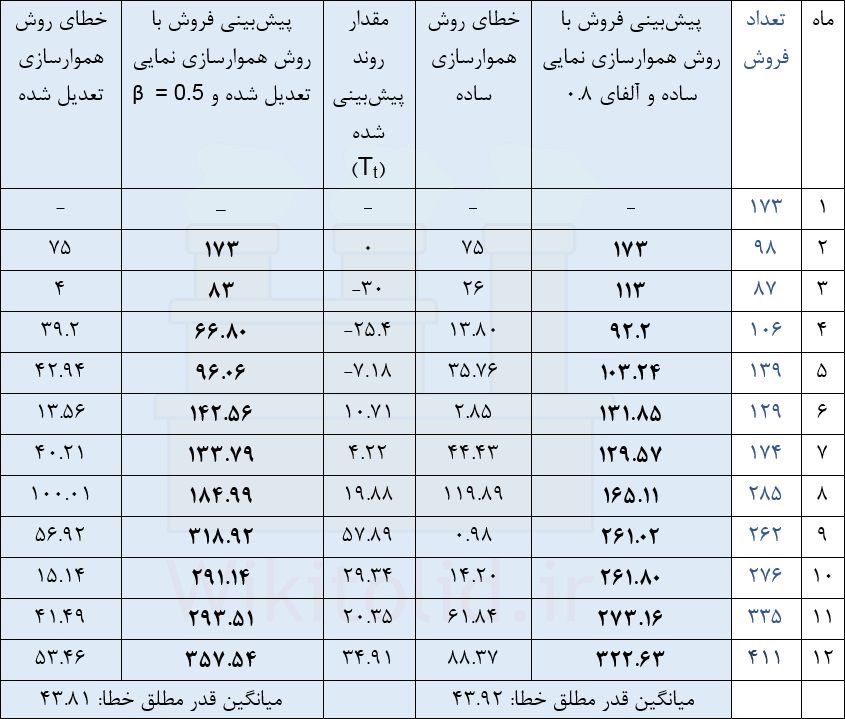
دادههای ستون اول (پیشبینی با آلفای ۰٫۸) با روش نمو هموار ساده محاسبه شدهاند و همان نتایجی هستند که در بخش اول درس به دست آوردیم.
برای جبران الگوی روند، کار را از ماه اول شروع میکنیم. برای ماه اول به دادههای قبلی دسترسی نداریم، پس لازم نیست آن را پیشبینی کنیم. برای ماه دوم، فرض کردیم روندی وجود ندارد و جای آن صفر گذاشتیم. وقتی تعداد دادهها زیاد است، میتوانیم این مقدار را صفر در نظر بگیریم تا خودش به تدریج، با طی دورههای بعدی، دقیقتر شود. اما اگر تعداد دادهها کم باشد میتوانیم متناسب با مقدار افزایش و کاهش مقادیر در هر دوره، یک مقدار حدودی درج کنیم تا سریعتر به دقت مناسب برسد.
نهایتاً مقدار پیشبینی شدهی نهایی (با تصحیح روند) از مجموع نتایج نمو هموار ساده و روندهای پیشبینی شده به دست میآید، مثلاً پیشبینی اولیه برای ماه دهم ۲۶۱٫۸۰ فروش بوده است و حدس زدیم که الگوی Trend بهاندازهی ۲۹٫۳۴+ روی آن اثر بگذارد، پس پیشبینی نهایی برابر ۲۹۱٫۱۴ خواهد بود.
هموار سازی نمایی با تصحیح روند در اکسل
برای استفاده از هموارسازی نمایی دوبل در اکسل باید فرمولنویسی بلد باشیم. با فرمولنویسی علاوه بر این روش، هر روش دیگری را هم میتوانیم در اکسل پیاده کنیم. برای همین، درس مستقلی را به پیادهسازی نمو هموار دوبل در اکسل اختصاص دادهایم، زیرا یادگیری آن میتواند برای استفاده از روشهای دیگر هم مفید باشد. برای مطالعه این درس روی لینک زیر کلیک کنید:

دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.