شما در حال خواندن درس راهکارهایی برای پیشبینی دادههای فصلی از مجموعه پیشبینی تقاضا هستید.
پیشبینی دادههای فصلی به راهکارهای ویژهای نیاز دارد. این دادهها به طور منظم در بعضی دورهها، تغییرات خاصی نشان میدهند. بنابراین لازم است پیشبینی خود را با این تغییرات هماهنگ کنیم تا به واقعیت نزدیکتر باشند. مثلاً فروش کاپشن در زمستان افزایش و در تابستان کاهش مییابد. تقاضا برای رستورانها و کافهها در ساعات غروب بیش از هنگام ظهر است. بازدید وبسایتهای علمی در تعطیلات آخر هفته کاهش مییابد. در این میان، بسیاری از روشهای کمی پیشبینی مثل: نمو هموار ساده، نمو هموار دوبل، رگرسیون خطی، میانگین ساده و میانگین متحرک نمیتوانند تغییرات فصلی دادهها را لحاظ کنند.
در این درس برای پیشبینی دادههای فصلی، دو راهکار ارائه خواهیم کرد:
راهکار اول، تعریف شاخصهای فصلی و اعمالشان بر نتایج پیشبینی است. مثلاً برای نرخ فروش کلاه پشمی، شاخص زمستان را ۱.۵ و شاخص تابستان را ۰.۲ انتخاب میکنیم. سپس بیتوجه به فصلی بودن دادهها، نرخ فروش را پیشبینی کرده و نتیجه را در شاخص فصلی مربوطه ضرب میکنیم.
راهکار دوم، غیرفصلی کردن دادهها است. یعنی دادههای هر فصل را بر شاخص آن فصل تقسیم میکنیم تا اصطلاحاً غیرفصلی شوند. با این کار تاثیر الگوی فصلی از دادهها حذف میشود و میتوانیم از روشهای عادی -که قابلیت لحاظ کردن الگوی فصلی را ندارند- برای پیشبینی استفاده کنیم. اما در آخر، متناسب با این که پیشبینی برای کدام دوره زمانی و کدام فصل انجام شده، شاخص همان فصل را اعمال میکنیم تا نتایج اصلاح شوند.
البته این دو راهکار در واقع اشکال مختلفی از یک روش واحد هستند و هر دو بر اساس شاخصهای فصلی کار میکنند. اما برای ارائهی شفافتر مطالب درس، مناسب دیدیم که آنها را به شکل بالا دستهبندی کنیم و ذیل دو عنوان مستقل ارائه دهیم.
راهکار اول:
پیشبینی دادههای فصلی به کمک شاخصهای فصلی
در جدول زیر، اطلاعات فروش روزانه یک محصول طی چهار هفته نشان داده شده است.
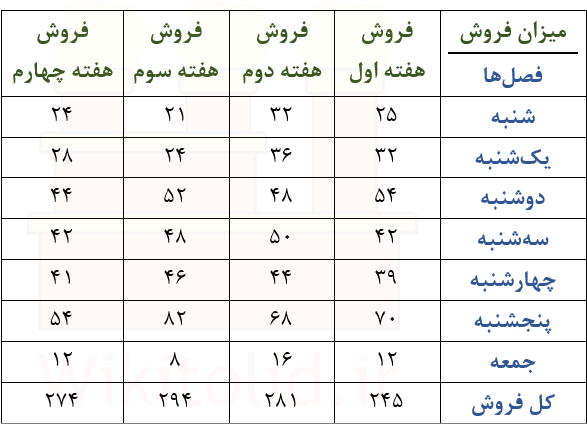
نمودار زیر، بر اساس اطلاعات جدول بالا رسم شده است و به وضوح میتوانیم فصلی بودن آن را ببینیم؛ فروش در روزهای پنجشنبه، افزایش قابل توجهی دارد و در روزهای جمعه به طور قابل توجهی کاهش مییابد.
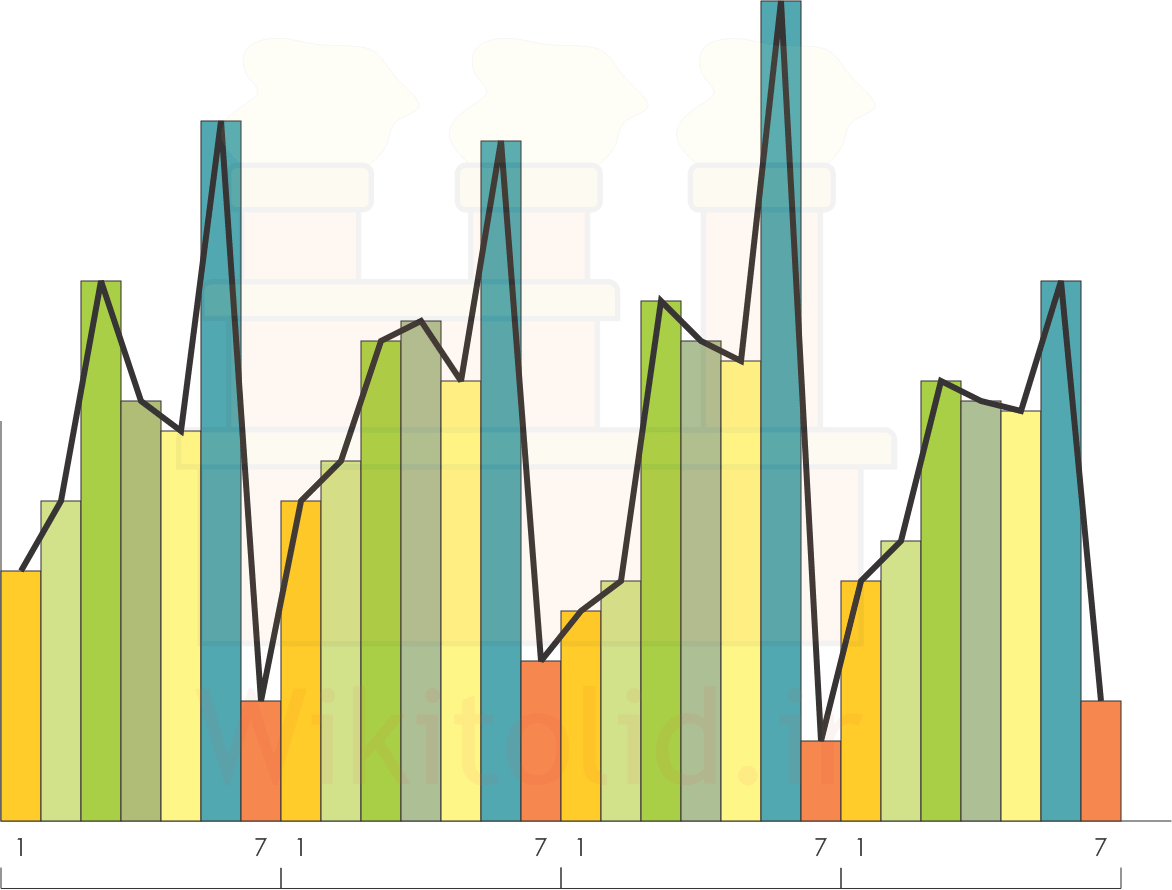
میخواهیم با تعیین شاخصهای فصلی، مقدار فروش در آینده را پیشبینی کنیم. برای این کار باید سه مرحله زیر را جلو ببریم:
کارهایی که باید انجام دهیم، شامل سه مرحلهی زیر میشوند.
مرحلهی اول: بررسی میکنیم که مقدار فروش در هر فصل -که در این مثال، روزهای هفته هستند- چند درصد از میانگین فروش روزانه است. مثلاً اگر متوسط فروش در هر روز ۱۰۰ واحد، در روزهای شنبه ۱۲۰ واحد و در روزهای جمعه ۴۰ واحد است، نتیجه میگیریم که شنبهها ۱۲۰ درصد و جمعهها ۴۰ درصد میانگین فروش را شامل میشوند. این مقادیر، شاخصهای فصلی هستند و با کمک آنها میتوانیم نتایج پیشبینی را اصلاح کنیم.
مرحلهی دوم: فرض میکنیم دادهها فصلی نیستند. با هر روشی که میخواهیم، حتی روشهایی که قدرت پیشبینی دادههای فصلی را ندارند، فروش در دورهی مورد نظر را پیشبینی میکنیم.
مرحلهی سوم: نتیجهای که از مرحلهی دوم به دست آوردهایم را در شاخص فصلی مربوطه ضرب میکنیم. مثلاً اگر مقدار فروش در روز جمعه از هفته پنجم را ۲۰۰ واحد پیشبینی کردهایم، آن را در شاخص روزهای جمعه که ۴۰% است ضرب میکنیم. با این کار مقدار پیشبینی شده متناسب با فصلی بودن دادهها اصلاح میشود.
در ادامه، بر اساس جدولی که بالاتر ارائه کردیم، پیشبینی را در سه مرحله انجام خواهیم داد.
مرحله اول: برای هر کدام از هفتههای اول تا چهارم، میانگین فروش روزانه را حساب میکنیم. مثلاً ابتدا بررسی میکنیم میانگین فروش روزانه در هفته اول چقدر بوده، بعد میانگین فروش روزانه در هفتههای دوم، سوم و چهارم را محاسبه می کنیم. سپس برای هفته اول حساب میکنیم که در هر روز، مقدار فروش چند درصد از میانگین فروش روزانه در هفته اول است. مقادیر به دست آمده، شاخصهای فصلی مربوط به روزهای هفته اول هستند.
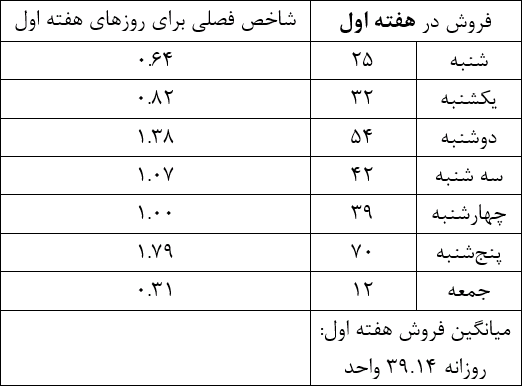
اقداماتی که گفتیم را برای هفتههای دوم، سوم و چهارم نیز انجام میدهیم و به جدول زیر میرسیم:
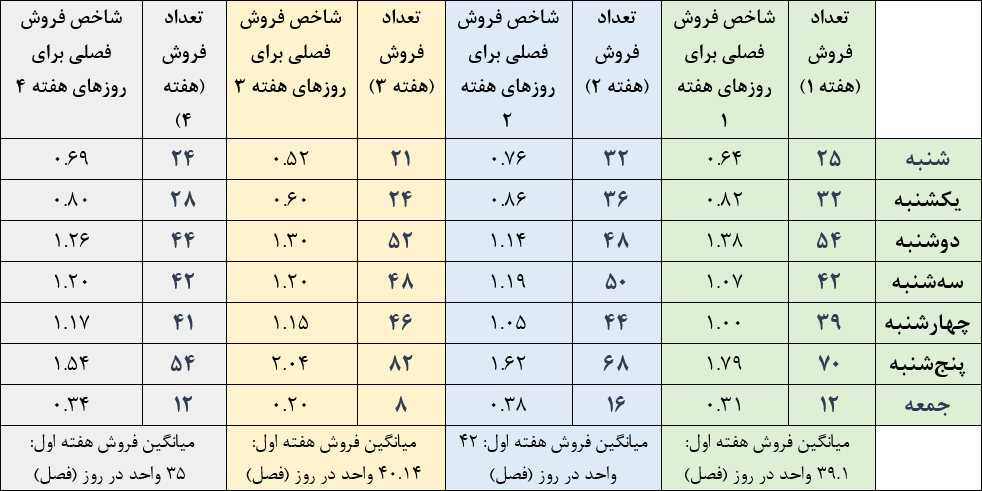
شاخصهایی که در جدول بالا نوشتیم برای هفتههای اول تا چهارم هستند، اما برای پیشبینی آینده باید شاخصهای هفتههای بعدی را هم محاسبه کنیم. مثلاً باید بدانیم شاخص هر کدام از روزها در هفتهی پنجم چقدر است.
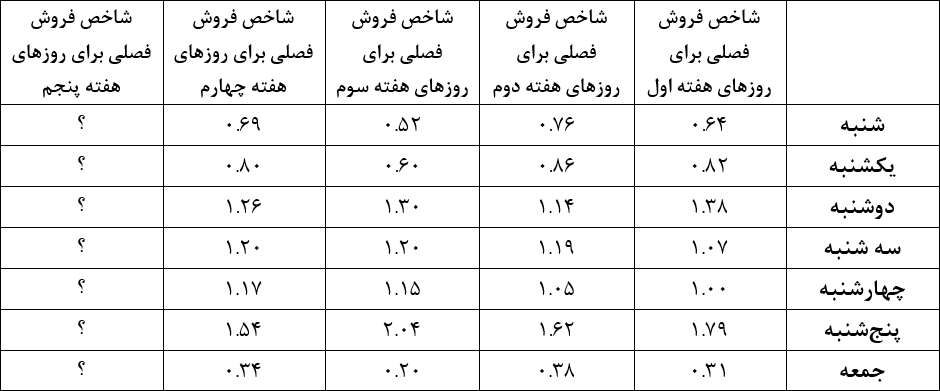
برای پیدا کردن شاخصها در هفتهی پنجم، باید روند تغییرات شاخصها در هفتههای قبل را لحاظ کنیم. مثلاً شاخص شنبهها در هفتههای اول تا چهارم برابر با ۰٫۶۴ و ۰٫۷۶ و ۰٫۵۲ و ۰٫۶۹ بود. بر اساس این دادهها میتوانیم شاخص روز شنبه در هفتهی پنجم را پیشبینی کنیم. در این مثال، برای پیشبینی شاخص روزهای هفتهی پنجم از روش میانگین ساده و روش نمو هموار (با آلفای ۰٫۶) استفاده کردیم. نتایج بسیار نزدیک هستند.
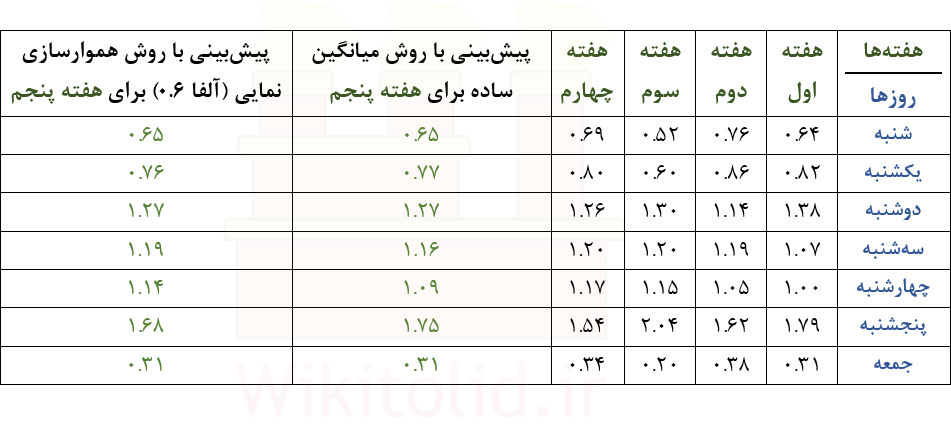
مرحله دوم: کارهایی که در مرحله قبل کردیم را کنار میگذاریم. هدف به دست آوردن شاخصها بود که انجام دادیم. در مرحله دوم فرض میکنیم دادهها فصلی نیستند. با این فرض، پیشبینی را با هر روشی که میخواهیم -و البته از نظرمان مناسب است- انجام میدهیم. مثلاً میتوانیم از روش میانگین ساده استفاده کنیم. در این حالت داریم:

مرحله سوم: مقادیری که در مرحله دوم پیشبینی کردیم را در شاخص فصلی مرتبط ضرب کنیم. مثلاً برای شنبه در هفتهی پنجم، شاخص ۰٫۶۵ بود. مطابق پیشبینی انجام شده در مرحله دوم، در هر روز از هفته پنجم به طور متوسط ۳۹.۰۷ واحد فروش داریم. این دو عدد را ضرب میکنیم و به ۲۵.۴ میرسیم. این عدد پیشبینی ما از مقدار فروش در روز شنبه از هفته پنجم است.
راهکار دوم:
غیرفصلی کردن دادهها
غیرفصلی کردن دادهها یعنی تأثیر فصلها بر تغییرات دادهها را حذف کنیم. برای این کار، شاخصهای فصلی را مثل بخش قبل محاسبه کرده، سپس دادههای هر فصل را بر شاخص آن فصل تقسیم میکنیم.
در بخش اول درس با چگونگی تعیین شاخصها آشنا شدیم. در این بخش از همان مثال استفاده میکنیم. در جدول زیر، شاخصهای فصلی محاسبه شدهاند.

از شاخصهای تعیین شده برای هر فصل میانگین میگیریم. مثلاً شاخص فصلی شنبهها در هفتههای اول تا چهارم را جمع کرده و بر چهار تقسیم میکنیم و به ۰.۶۵ میرسیم. همین کار را برای تمام فصلها -روزهای هفته- انجام میدهیم.
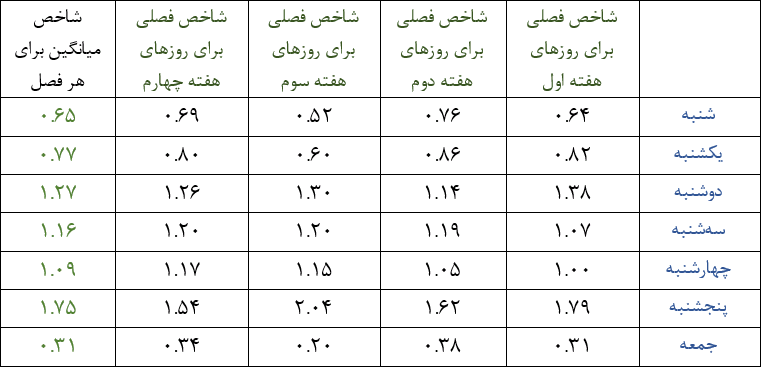
مقدار فروش هر روز را بر شاخص میانگین آن روز تقسیم میکنیم و به جدول زیر میرسیم. البته اگر مقادیر را دستی حساب کنیم، ممکن است با جدول زیر متفاوت باشد؛ علت این است که شاخصها را در جدول بالا گرد کردیم، مثلاً ۰.۶۵۲۵ را ۰.۶۵ نوشتیم. اما در عمل محاسبات را با دقت چهار رقم اعشار انجام دادیم، یعنی ۲۵ را بر ۰.۶۵ تقسیم نکردیم، بلکه بر ۰.۶۵۲۵ تقسیم کردیم. دادههای جدول زیر غیرفصلی هستند.
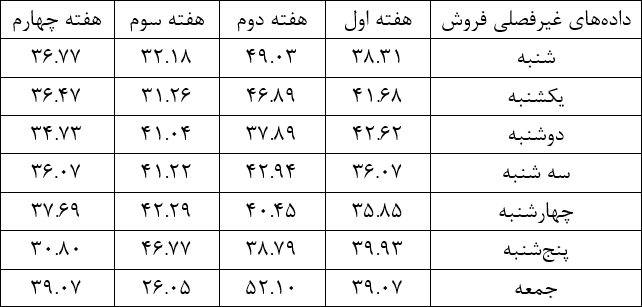
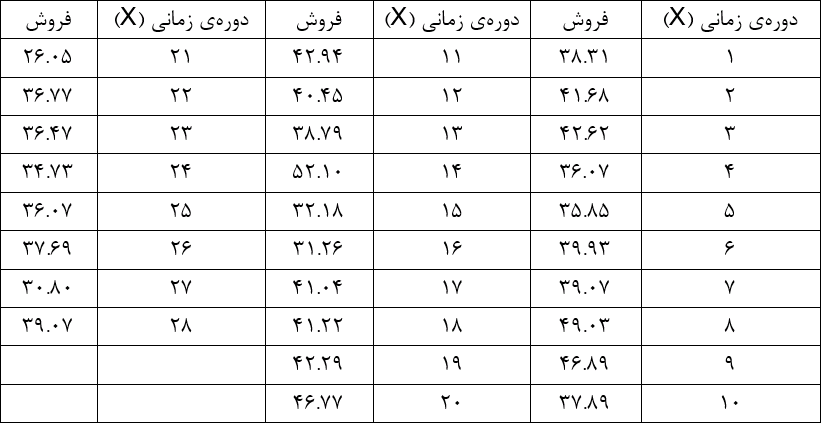
برای پیشبینی دادههای غیرفصلی، روشهای زیادی وجود دارد. در این مثال از رگرسیون خطی تک متغیره برای پیشبینی استفاده خواهیم کرد. دورهها را شمارهگذاری میکنیم:
روش محاسبه رگرسیون را در یک درس دیگر توضیح دادهایم و از تکرار مطالب خودداری میکنیم. با رگرسیون خطی به تابع زیر میرسیم:
![]()
پارامتر X شماره دورهی مورد نظرمان است که اگر آن را در رابطه وارد کنیم، مقدار فروش در آن دوره به دست میآید. برای مثال اگر بخواهیم مقدار فروش در روز شنبه از هفته پنجم را پیشبینی کنیم، جای X مقدار ۲۹ میگذاریم؛ در این حالت مقدار فروش برابر ۳۵٫۹ واحد محاسبه میشود. در قدم بعد باید این عدد را در شاخص میانگین روزهای شنبه ضرب کنیم؛ بنابرین ۳۵.۹ را در ۰.۶۵۲۵ ضرب میکنیم و به ۲۳.۳ میرسیم.


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.