شما در حال خواندن درس رگرسیون خطی برای تشخیص روابط علی از مجموعه پیشبینی تقاضا هستید.
در این درس، روش رگرسیون خطی یکمتغیره و چند متغیره را به عنوان نمونهای از روشهای علی برای شناسایی ارتباط یک پارامتر وابسته یا به یک یا چند پارامتر مستقل بررسی خواهیم کرد. بنابراین در بحث پیشبینی تقاضا با کمک این روش میتوانیم ارتباط تقاضا با پارامترهای دیگر مثل «قیمت محصول» و «میزان تبلیغات» را به شکل رابطه ریاضی توصیف کنیم. مثلاً رابطهای که با این روش به دست میآوریم، نشان میدهد که اگر قیمت محصول دو برابر شود، تقاضا چقدر کاهش مییابد. یا اگر قیمت محصول ۲۰٪ افزایش پیدا کند، اما برای تبلیغات ۴۰٪ بیشتر هزینه کنیم، تقاضا چگونه تغییر خواهد کرد.
برای این که رابطه ریاضی میان تقاضا و پارامترهای دیگر را بیابیم، دو حالت قابل تصور است. حالت اول این که فقط در صدد یافتن ارتباط تقاضا با «یک پارامتر دیگر» باشیم. در این درس، روش رگرسیون خطی تک متغیره را برای این حالت معرفی میکنیم؛ البته این روش فقط میتواند ارتباط پارامترها را به شکل یک معادله خطی توصیف کند. حالت دیگر این است که بخواهیم ارتباط تقاضا با «چند پارامتر دیگر» را بیابیم. در این درس روش رگرسیون خطی دو متغیره را برای شناسایی رابطه خطی «تقاضا» با «دو پارامتر دیگر» ارائه خواهیم کرد. همچنین با صرفنظر از محاسبات ریاضی، روش اجرای رگرسیون خطی چند متغیره در اکسل را توضیح خواهیم داد.
پارامترهای وابسته و مستقل
برای مطالعه این درس باید منظور از پارامتر وابسته و پارامتر مستقل را بدانیم. برای درک این پارامترها یک مثال ساده میزنیم. به نظرتان چه عواملی باعث موفقیت یک ازدواج میشوند؟ صداقت؟ وفاداری؟ پول؟ اگر این سه پارامتر موثر باشند، یعنی موفقیت در ازدواج یک پارامتر وابسته و صداقت، وفاداری و پول پارامترهای مستقل هستند. به پارامترهای مستقل و وابسته، علت و معلول نیز میگویند.
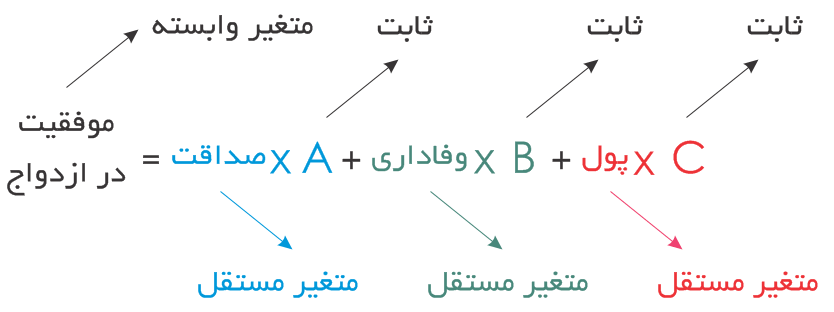
اگر بخواهیم موفقیت در ازدواج و دلایل آن را با روابط ریاضی نشان دهیم، شبیه زیر خواهد بود. البته با این فرض که بتوانیم برای پول، وفاداری، صداقت و موفقیت ارزش عددی تعریف کنیم.

رابطه بالا به اندازه کافی دقیق نیست؛ زیرا پول، وفاداری و صداقت به یک اندازه روی موفقیت در ازدواج تأثیر ندارند. برای همین میتوانیم برای هر کدام از پارامترهای مستقل، ضریب تعیین کنیم. البته رابطهای که نوشتیم یک رابطه خطی ساده است، حال آن که میتوانستیم آن را به شکل غیرخطی هم توصیف کنیم.
توابع خطی و غیرخطی
تابعی که در بخش قبل برای موفقیت در ازدواج مثال زدیم، خطی بود. اما بسیاری از توابع، غیرخطی هستند. برای پیشبینی ارتباط میان تقاضا و عوامل دیگر، میتوانیم ارتباطشان را خطی یا غیرخطی فرض کنیم. استفاده از توابع خطی سادهتر است، اما توابع غیرخطی دقیقتر میتوانند تقاضا را پیشبینی کنند. توابع چند جملهای با درجهی دو و بالاتر، همچنین توابع نمایی، لگاریتمی، مثلثاتی، مدولوس، نسبی و چند جملهای غیرخطی هستند. مثلاً تابع زیر غیرخطی است. در این درس فرض میکنیم که توابع خطی میتوانند به خوبی ارتباط تقاضا با پارامترهای دیگر را توصیف کنند.

روش رگرسیون خطی تک متغیره (کمترین مجذورات)
روش «رگرسیون خطی تک متغیره» یا «کمترین مجذورات» فقط ارتباط پارامتر وابسته با یک پارامتر مستقل را به شکل خطی توصیف میکند. بنابراین این روش زمانی مفید است که بخواهیم ارتباط تقاضا با عاملی مثل قیمت را بیابیم و از سایر عوامل صرفنظر کنیم.
در ادامه چگونگی استفاده از رگرسیون خطی تک متغیره را با کمک مثال توضیح خواهیم داد. نمودار زیر ارتباط قیمت یک محصول با مقدار فروش آن را نشان میدهد. هدف این است که با اطلاعات این نمودار، رابطه ریاضی میان مقدار فروش و قیمت محصول را شناسایی کنیم.
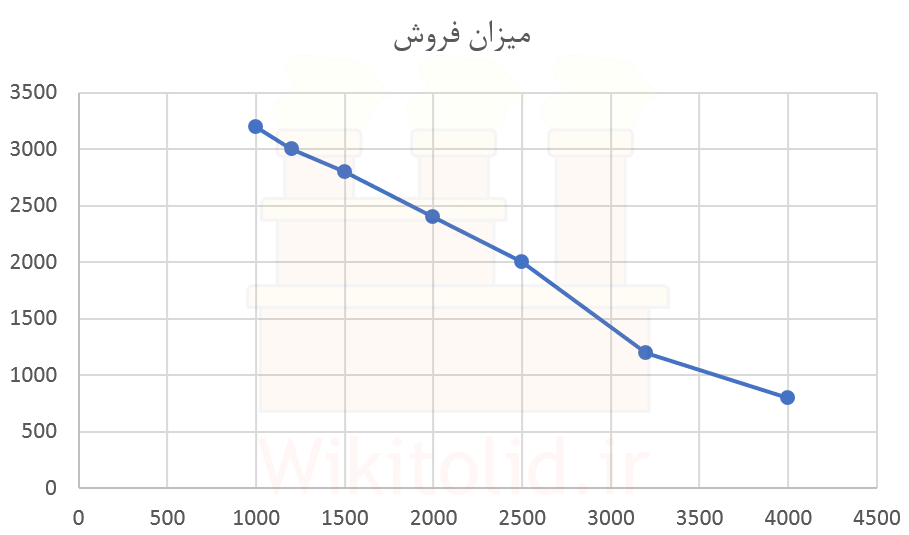
گفتیم روش رگرسیون خطی، ارتباط میان دو پارامتر را به شکل رابطه خطی توصیف میکند. آیا یک رابطه خطی میتواند توصیف خوبی از نمودار بالا و تغییرات آن در آینده باشد؟ در نمودار بالا، تغییرات فروش نسبت به زمان به خط صاف نزدیک است. برای همین به نظر میرسد که فرض خطی بودن رابطه فروش با قیمت، چندان دور از واقعیت نیست؛ برای همین استفاده از روش رگرسیون خطی میتواند توجیهپذیر باشد.
مطابق نمودار، جدول زیر را تشکیل میدهیم تا به اطلاعات عددی مربوط به میزان فروش و قیمت محصول دسترسی داشته باشیم.
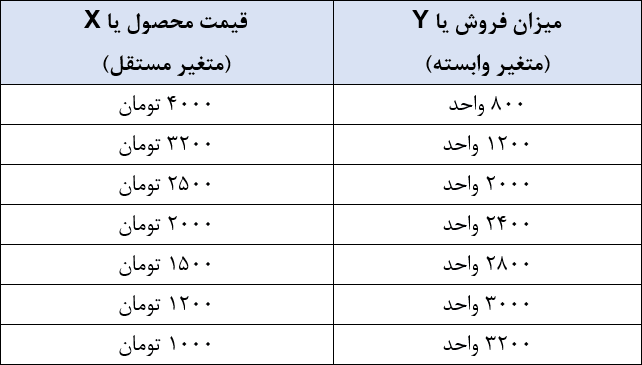
برای استفاده از رگرسیون خطی، باید رابطه «فروش» و «قیمت» را خطی فرض کنیم. پس شکل کلی رابطه F=a+bX خواهد بود. F بیانگر مقدار فروش در آینده و X بیانگر قیمت محصول است. F و X متغیر هستند و میتوانیم مقادیر مختلفی را به جای آنها قرار دهیم، اما a و b دو عدد ثابت هستند که باید آنها را با روابط زیر محاسبه کنیم:
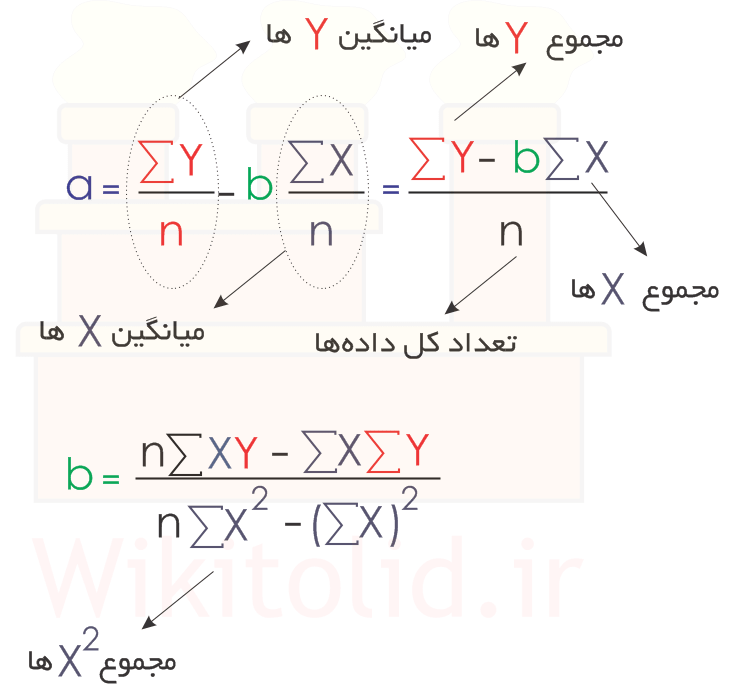
برای استفاده از روابط بالا، جدول را بهصورت زیر تکمیل میکنیم.
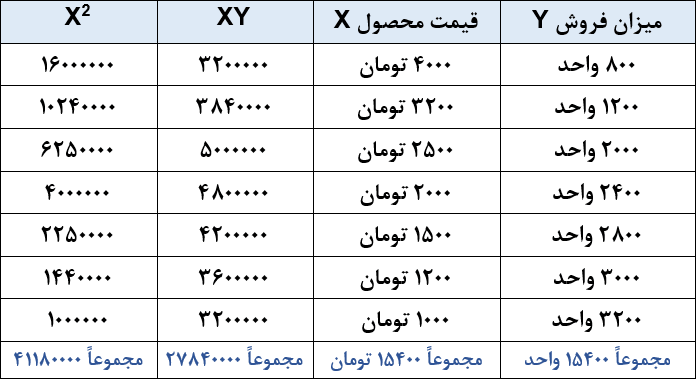
با جاگذاری مقادیر در روابط بالا، a و b به دست میآید.

گفتیم رابطه مقدار فروش پیشبینی شده (F) با قیمت فروش (X) از رابطه F=a+bX تبعیت میکند، بنابراین با جاگذاری a و b داریم:
![]()
برای ارزیابی رابطهای که به دست آوردهایم میتوانیم از «ضریب همبستگی» و «ضریب تعیین» استفاده کنیم.
ضریب همبستگی (r) با رابطه زیر به دست میآید. مقدار آن بین -۱ و ۱ است و هر چه به صفر نزدیکتر باشد، یعنی رفتار پارامترها همخوانی کمتری با یکدیگر دارد. مثبت بودن مقدار r بیانگر رابطهی مستقیم بین پارامترها و مقدار منفی نشانه رابطهی معکوس آنها است.
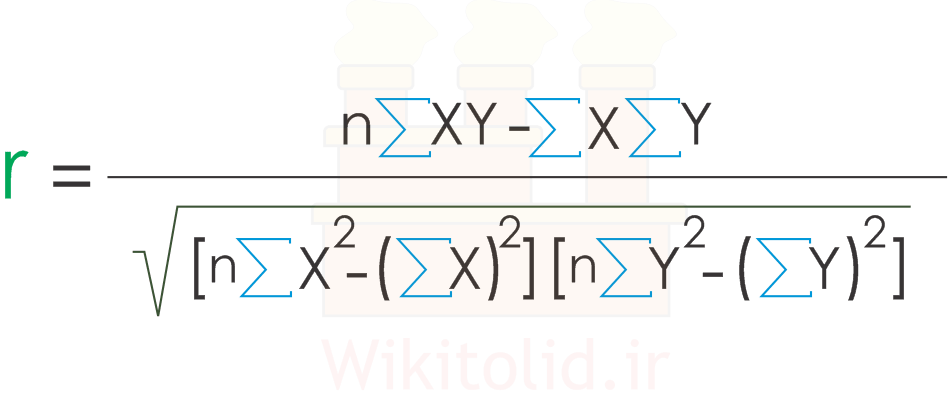
ضریب تعیین را میتوانیم با مجذور کردن ضریب همبستگی (یعنی به توان دو رساندن آن) محاسبه کنیم. این ضریب نشان میدهد که رفتار پارامتر وابسته تا چه اندازه با رفتار پارامتر مستقل همخوانی دارد. مثلاً اگر مقدار آن ۰.۸ باشد، یعنی پارامتر وابسته ۸۰٪ با تغییرات رفتار پارامتر مستقل همخوانی دارد و ۲۰٪ عدم همخوانی از سایر عوامل نشأت گرفته است. اگر مقدار ضریب تعیین کم باشد، مثلاً کمتر از ۰.۵ باشد، بهتر است پیشبینی را بر اساس پارامتری دیگر انجام دهیم. همچنین میتوانیم جای رگرسیون تکمتغیره، از رگرسیون چند متغیره استفاده کنیم و سایر عوامل را نیز در نظر بگیریم؛ با این کار ضریب تعیین افزایش مییابد و به نتایج مطمئنتری میرسیم.
استفاده از رگرسیون خطی یک متغیره در اکسل
برای استفاده از رگرسیون خطی یک متغیره در اکسل، مقادیر دو ستون X و Y را ثبت میکنیم.
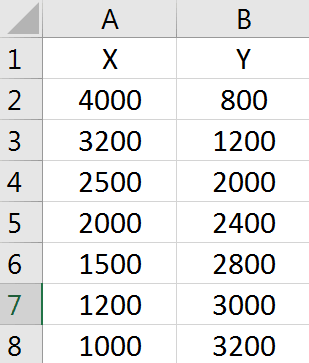
از منوی Insert و از بخش Charts روی Scatter کلیک میکنیم.
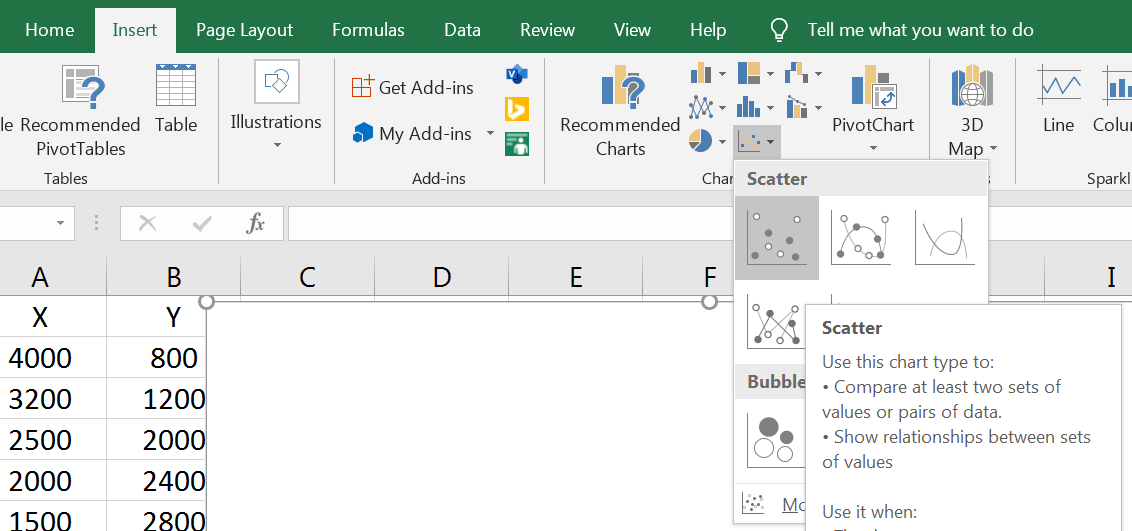
نشان ماوس را روی جعبهی سفیدی که باز شده میبریم و Select Data را انتخاب میکنیم.
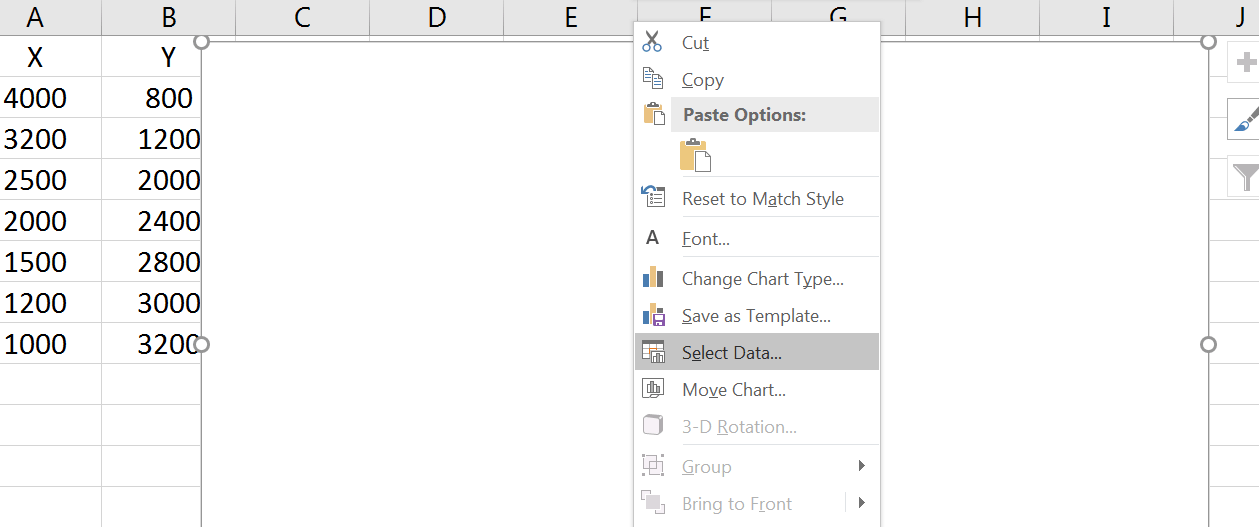
در پنجرهی باز شده، اگر در جعبههای چپ و راست مقداری وجود دارد، با دکمهی Remove پاک میکنیم، سپس روی Add کلیک میکنیم.
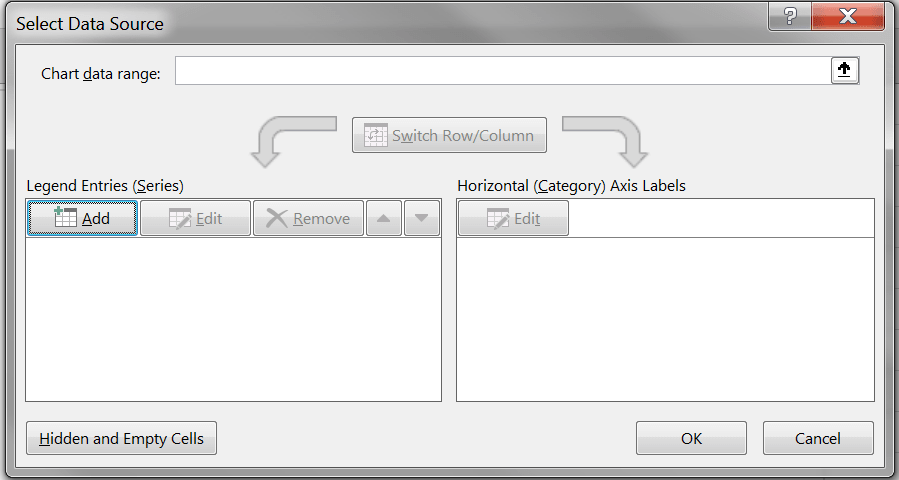
در پنجره جدید، عنوان نمودار را در فیلد اول مینویسیم. در فیلد دوم مقادیر عددی ستون X و در فیلد سوم مقادیر Y را انتخاب میکنیم.
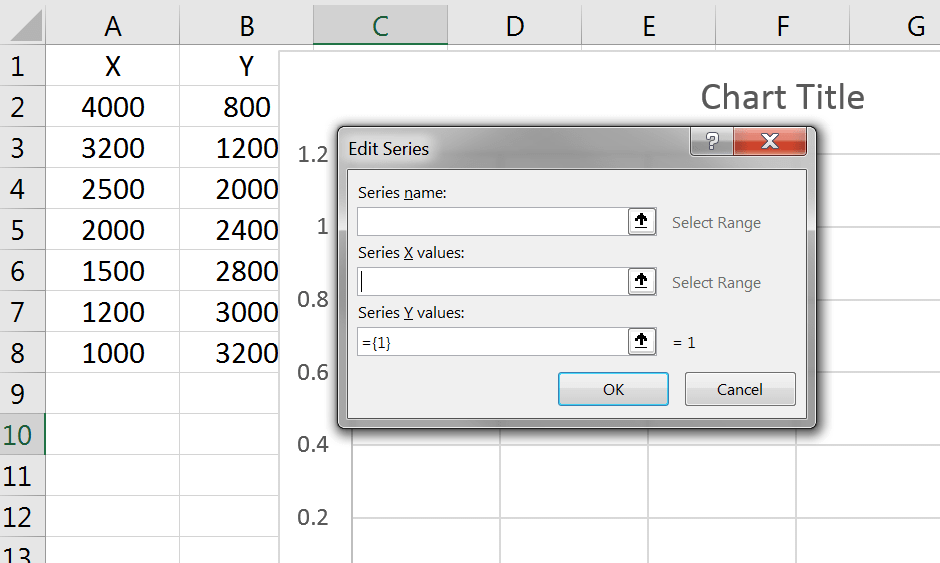
مثلاً برای فیلد دوم، روی دکمهی کوچک سمت راست کلیک میکنیم و در ستون X، مقادیر ۴۰۰۰ تا ۱۰۰۰ را انتخاب میکنیم:
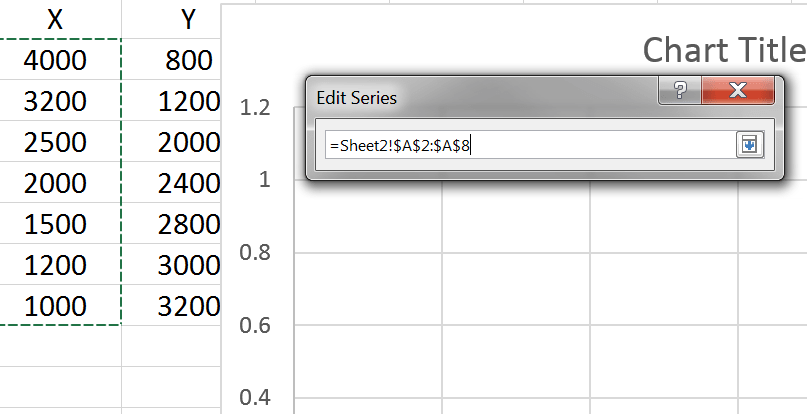
بعد از انتخاب مقادیر مربوط به ستونهای X و Y، دادهها بهصورت نقطهای نمایش داده میشوند. این نقاط همان مقادیر جدول هستند و چیز جدیدی را نمایش نمیدهند.
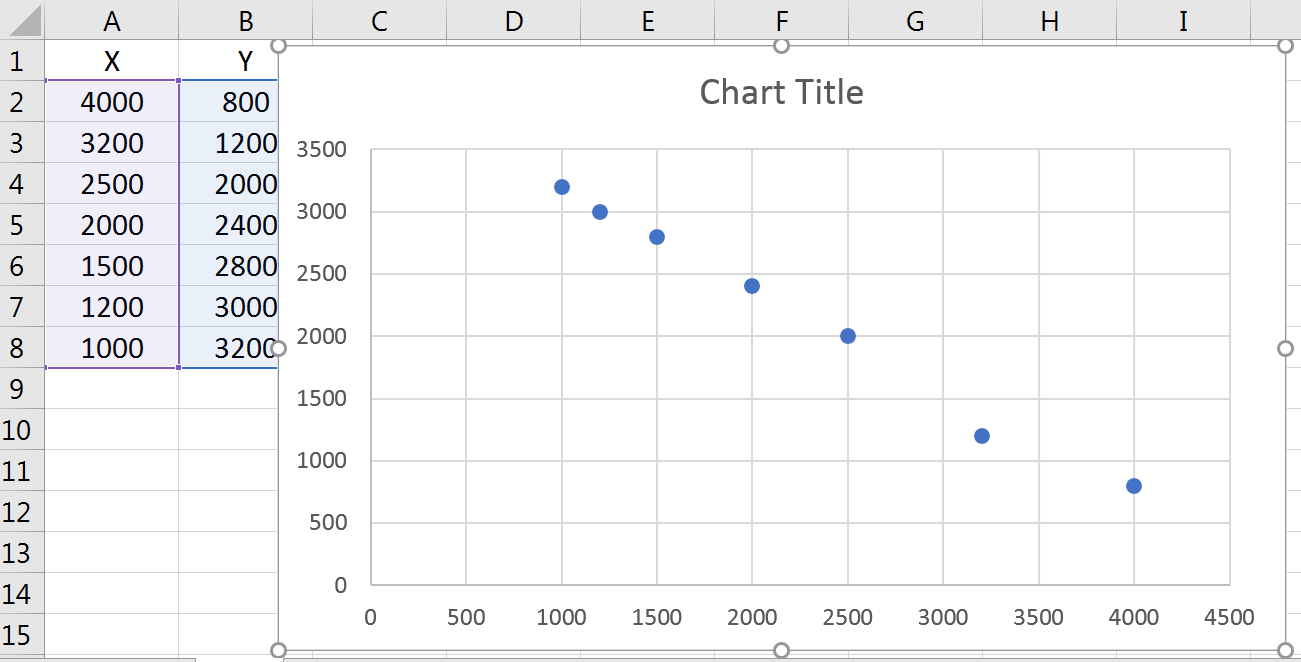
روی نمودار کلیک میکنیم و از Design، گزینه Add Chart Element را انتخاب کرده، منوی Trendline را باز میکنیم.
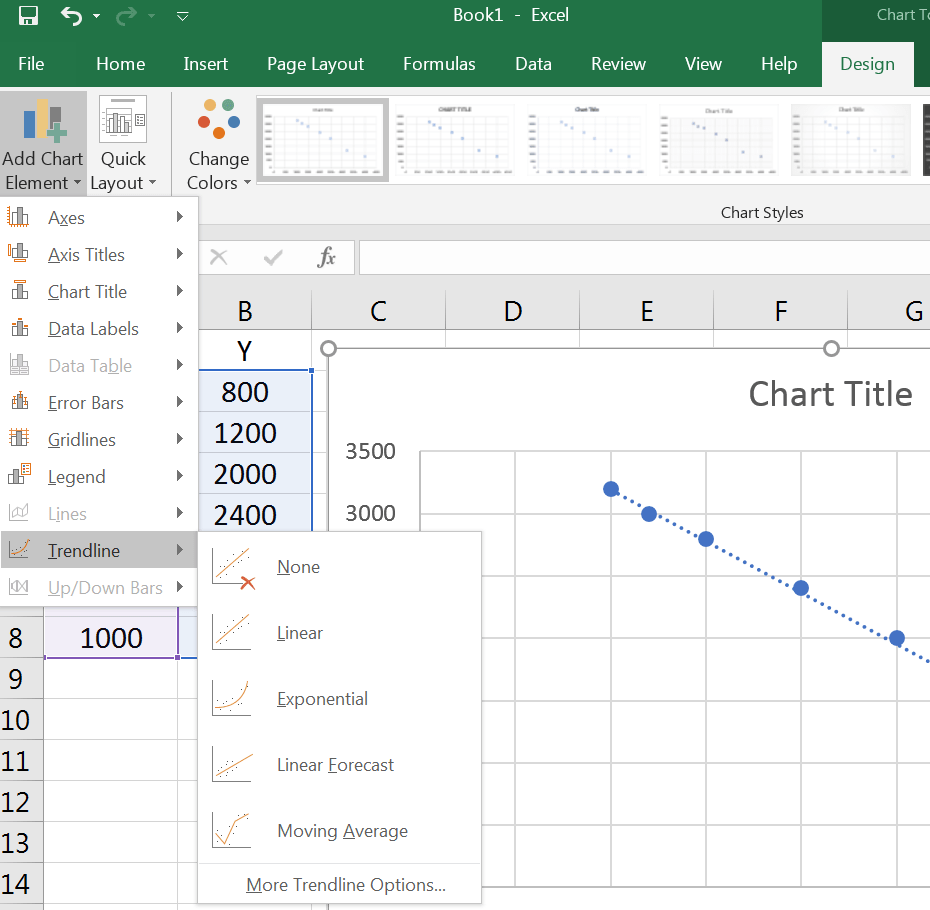
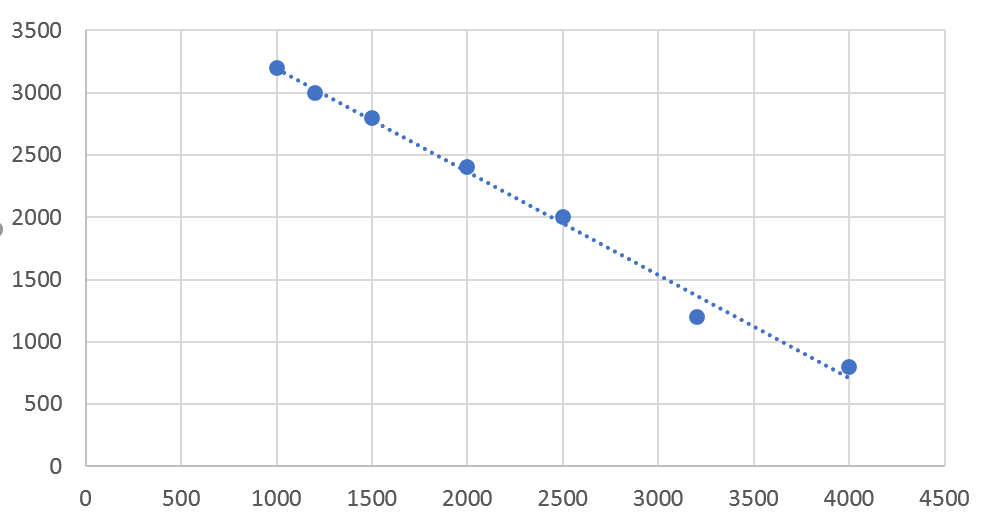
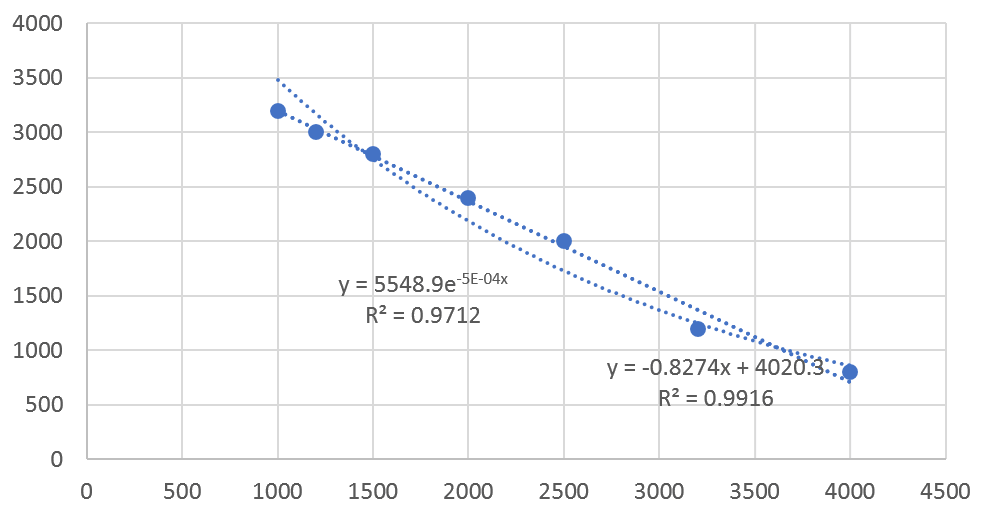
اگر روی Linear کلیک کنیم، پیشبینی بر اساس تابع خطی انجام میشود. اگر Exponential را انتخاب کنیم، پیشبینی بر اساس تابع نمایی انجام میشود. در تصویر زیر گزینه Linear را انتخاب کردهایم.
از منوی Trendlines گزینهی Exponential را انتخاب میکنیم تا نمودار نمایی هم ببینیم.
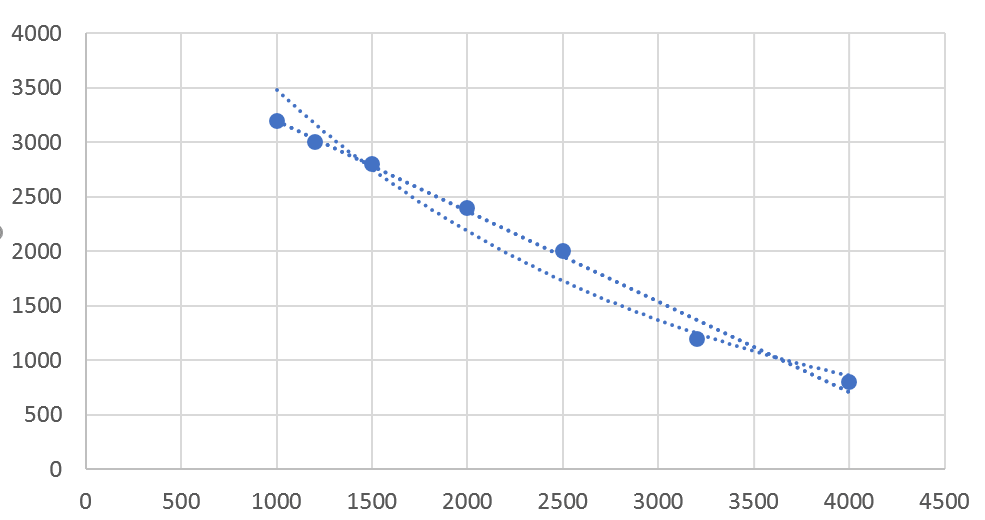
به جز نمودار، تمایل داریم به رابطههای پیشبینی شده برای فروش و قیمت محصول دسترسی داشته باشیم. پس روی یکی از خطوط پیشبینی شده کلیک راست کرده و گزینهی Format Trendlines را انتخاب میکنیم.
این کار را برای هر دو نمودار خطی و نمایی انجام میدهیم تا روابط مربوط به آنها ثبت شود. همچنین در زیر روابط ریاضی، ضریب تعیین هم نوشته میشود. همانطور که در بخش قبل اشاره کردیم، این ضریب بیانگر میزان همخوانی رفتار پارامترها است.
آیا میتوانیم برای دادههای زمانی از رگرسیون استفاده کنیم؟
روشهای کمی پیشبینی به دو دسته زمانی و علی تقسیم میشوند. روشهای زمانی برای پیشبینی دادههایی هستند که بر اساس زمان مرتب شدهاند. اما روشهای علی برای توصیف رابطه رباضی میان تقاضا و عوامل دیگر هستند. روشهای علی مثل رگرسیون میتوانند برای سریهای زمانی هم استفاده شوند. این روشها، رابطه تقاضا با عوامل دیگر را شناسایی میکنند و «زمان» میتواند یکی از این عوامل باشد. جدول زیر فروش یک محصول طی دوازده ماه را نشان میدهد و یک سری زمانی است. فرض کنید میخواهیم از رگرسیون خطی برای پیشبینی فروش آینده استفاده کنیم.
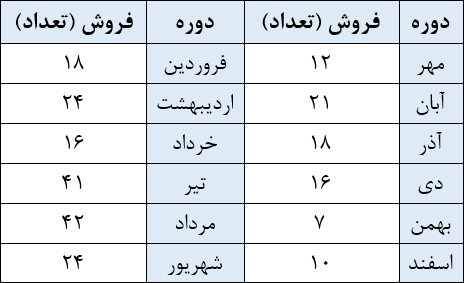
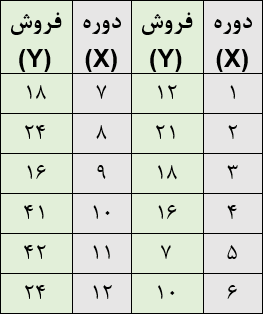
در این مثال، مقدار فروش یا Y پارامتر وابسته و زمان پارامتر مستقل است. برای این که بتوانیم دورههای زمانی را به عدد تبدیل کنیم و رابطهشان با تقاضا را بیابیم، دورهها را شمارهگذاری میکنیم. این شمارهها مقادیر پارامتر X هستند. با کمک رگرسیون، رابطه ریاضی بین Y و X را پیدا میکنیم. سپس میتوانیم در رابطهای که به دست میآید، مقادیر مختلف X را جاگذاری کرده و فروش دورههای آینده را پیشبینی کنیم.
رگرسیون خطی دو متغیره
رگرسیون خطی دو متغیره میتواند رابطه یک پارامتر وابسته مثل تقاضا را با دو پارامتر مستقل مثل «قیمت» و «هزینه تبلیغات» توصیف کند. البته از نظر ریاضی فرقی ندارد که چند پارامتر مستقل داشته باشیم و همه این حالتها با روش مشابهی حل میشوند. با این وجود، محاسبات ریاضی در حالتی که بیش از دو پارامتر مستقل داریم، پیچیده هستند. برای همین فقط نحوه محاسبه رگرسیون دو متغیره را توضیح میدهیم و برای حالتی که تعداد متغیرها بیشتر است، از نرمافزار اکسل استفاده خواهیم کرد.
در جدول زیر مقدار تقاضا در ارتباط با پارامتر قیمت و پارامتر هزینه معرفی کالا درج شده است. در ادامه با استفاده از رگرسیون دو متغیره، رابطه ریاضی مقدار فروش با قیمت و هزینه معرفی کالا را شناسایی خواهیم کرد.
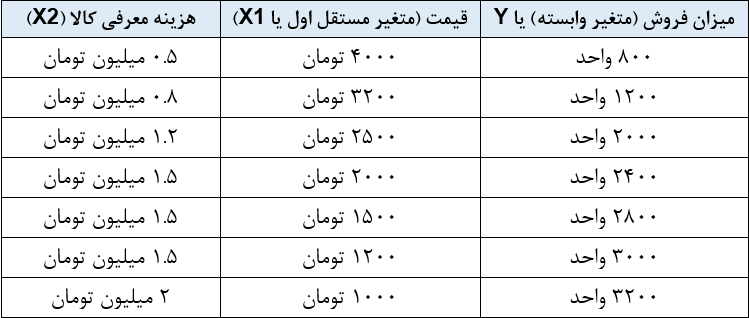
در این حالت، تابع فروش (F) مشابه زیر است و باید مقادیر a و b1 و b2 را برای آن پیدا کنیم.

هر یک از ضرایب a و b1 و b2 با روابط زیر به دست میآیند:
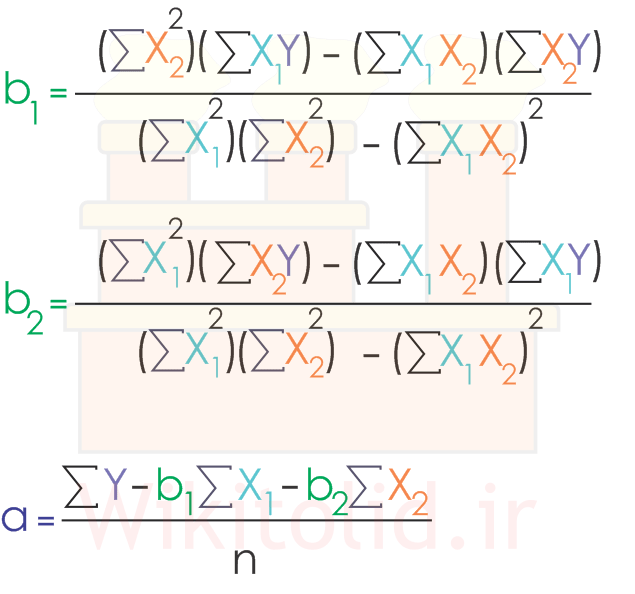
جدول برای استفاده از روابط بالا به شکل زیر تکمیل میکنیم.
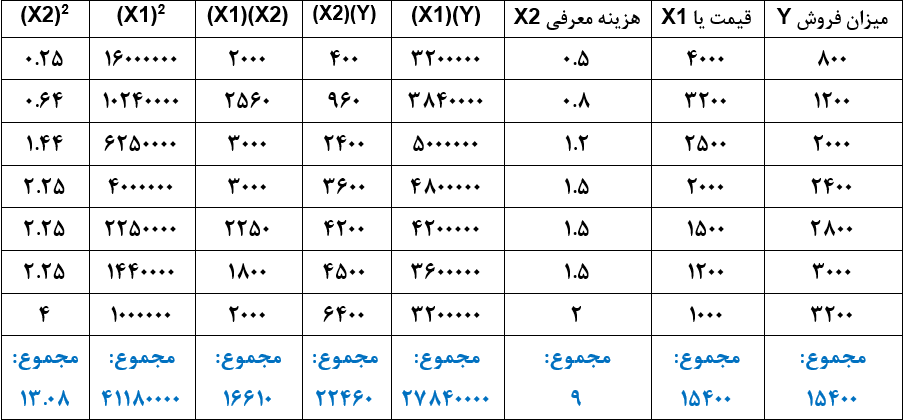
با جاگذاری مقادیر داریم:
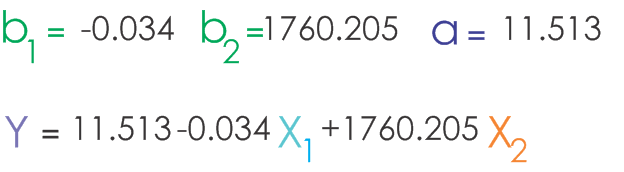
استفاده از رگرسیون خطی چند متغیره در اکسل
رگرسیون خطی چند متغیره میتواند ارتباط یک پارامتر وابسته مثل تقاضا را با دو یا چند پارامتر مستقل مثل قیمت محصول، نرخ تورم و هزینه تبلیغات به شکل خطی شناسایی کند. برای استفاده از این روش در اکسل، ابتدا باید ابزار تحلیل رگرسیون را فعال کنیم. برای این کار از منوی File به Options میرویم و روی Add-ins کلیک میکنیم. در Manage، گزینهی Excel Add-ins را انتخاب و روی Go کلیک میکنیم.
گزینهی Analysis Toolpak را فعال میکنیم تا ابزارهای رگرسیون فعال شوند.
فرض کنید میخواهیم رابطهی فروش با چهار متغیر مستقل X1 تا X4 را بر اساس اطلاعات جدول زیر محاسبه کنیم.
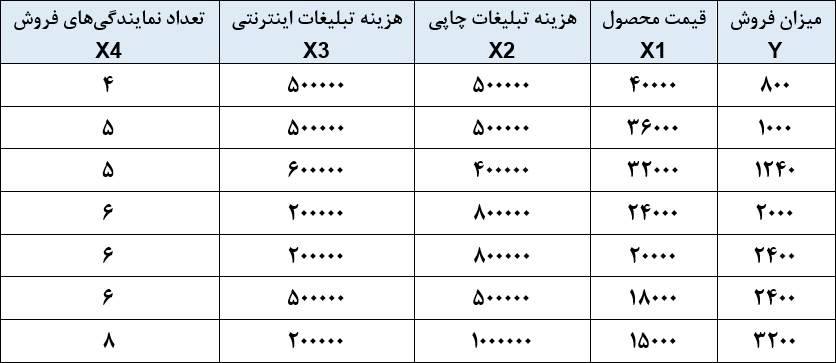
ابتدا اطلاعات جدول را ثبت میکنیم.
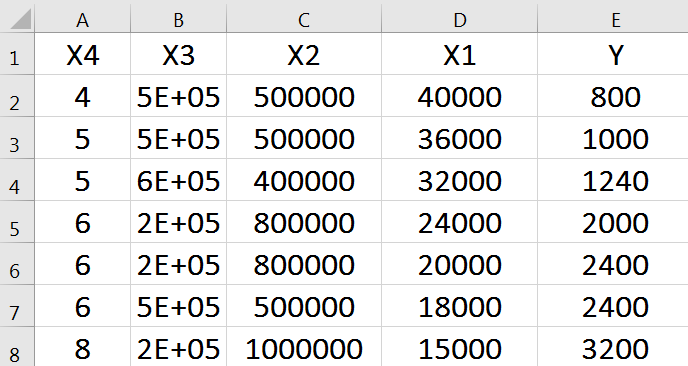
در منوی Data روی Data Analysis کلیک کرده و در پنجرهی باز شده، Regression را انتخاب میکنیم.
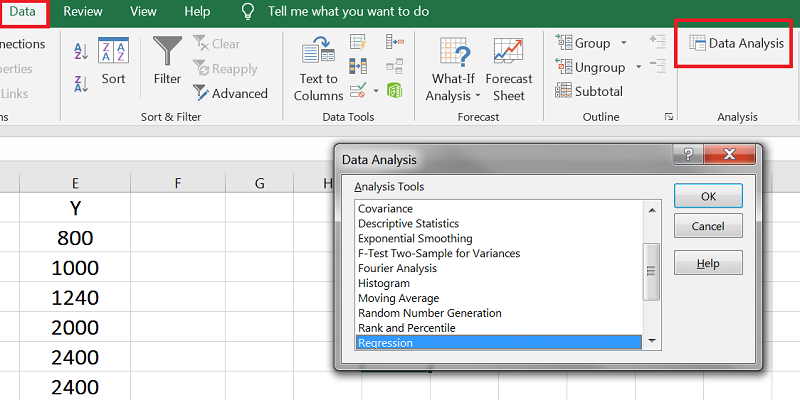
پس از فشردن دکمهی OK یک پنجره جدید باز میشود.
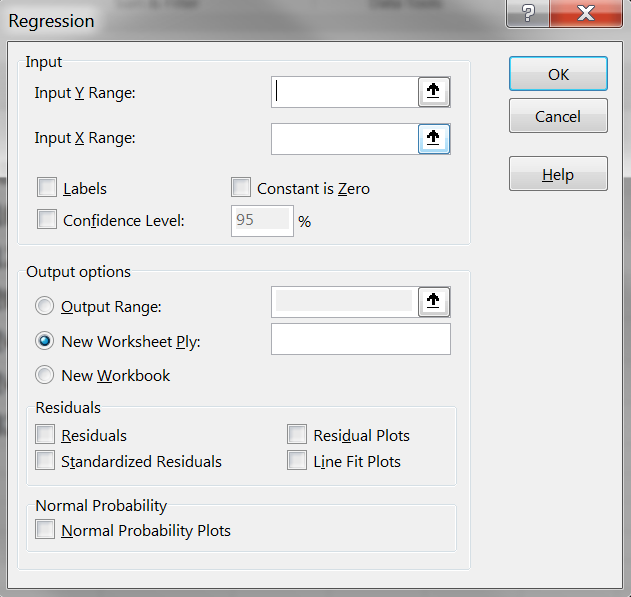
در فیلد اول (Input Y Range)، باید مقادیر ستون Y را انتخاب کنیم.
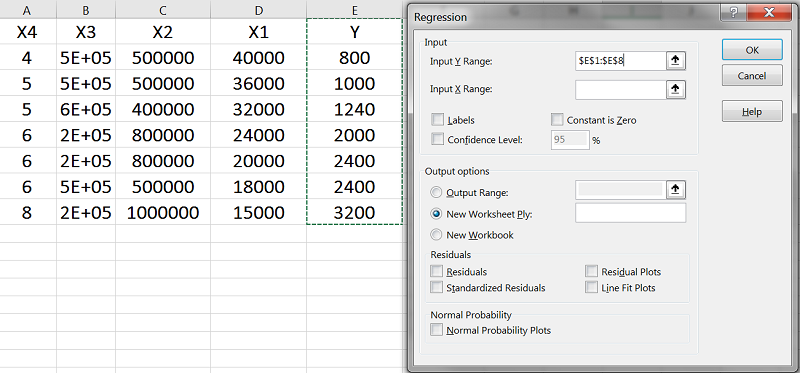
در فیلد دوم (Input X Range)، مقادیر مربوط به X1 تا X4 را انتخاب میکنیم.
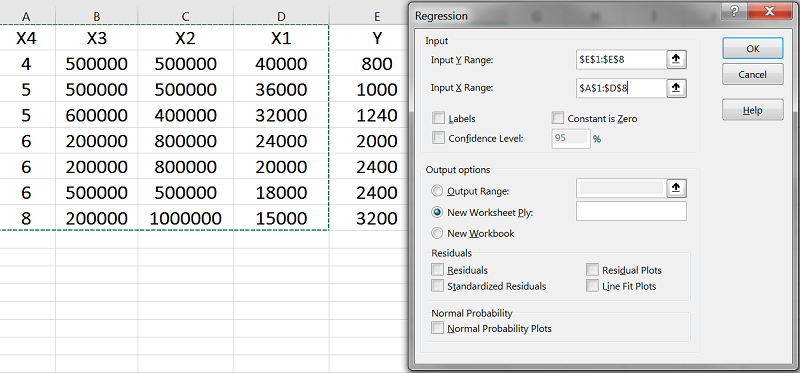
تیک Labels را فعال میکنیم تا برای سیستم تعریف شود که X1 و X2 و X3 و X4 عنوان ستونها هستند. در Output Range مشخص میکنیم که نتایج در کدام سلول نمایش داده شوند. این فیلد تأثیری در تحلیلمان ندارد و فقط محل نمایش نتایج را تعیین میکند. هر سلولی که انتخاب کنیم، نتایج تحلیل در سمت چپ و پایین آن نمایش داده خواهد شد.
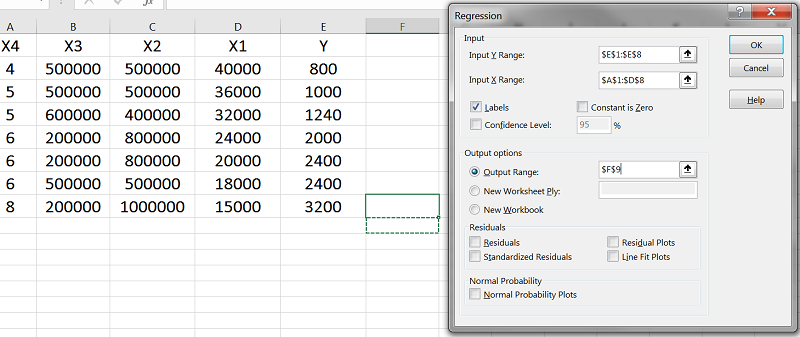
روی OK کلیک میکنیم تا نتایج تحلیل رگرسیون نمایش داده شوند.
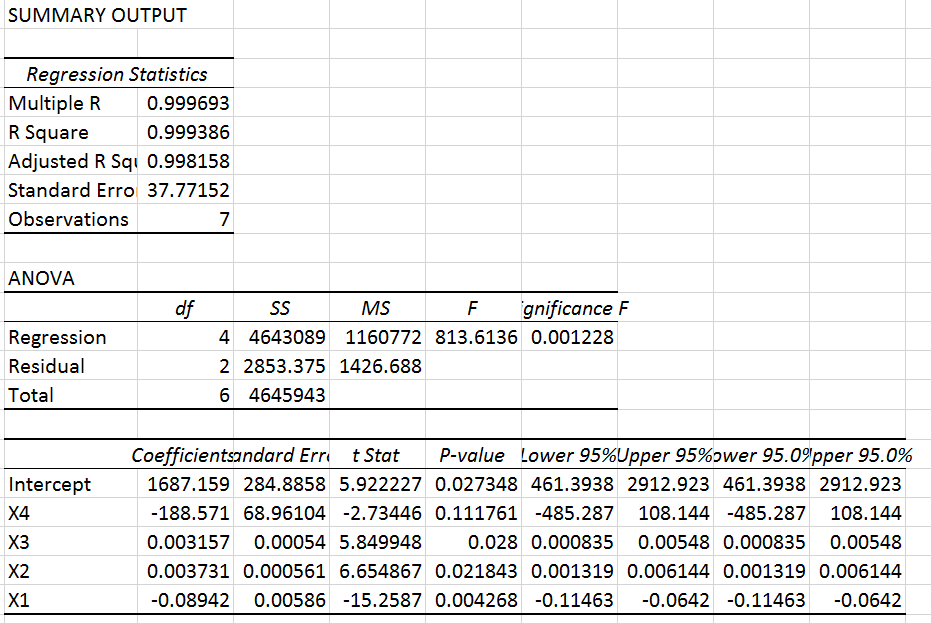
در بخش قبل گفتیم برای سنجش ارتباطی که شناسایی کردهایم، میتوانیم از ضریب تعیین (مجذور ضریب همبستگی) استفاده کنیم. در بخش Regression Statistics میبینیم که مقدار R-Square یا ضریب تعیین برابر ۰٫۹۹۹ درج شده، یعنی تغییرات فروش همخوانی زیادی با تغییرات پارامترهای مستقل دارند. پایینتر میبینیم که مقادیری برای Intercept و X4 تا X1 مشخص شده است. Intercept همان a و X4 تا X1 مقادیر b4 تا b1 هستند. بنابراین رابطه میزان فروش با چهار پارامتر دیگر به صورت زیر است:


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.