فرایند تحلیل سلسله ‌مراتبی (Analytic Hierarchy Process یا AHP)

تکنیک AHP برای وزن‌دهی به معیارها (همراه با تست سازگاری)

همانطور که گفتیم، وزن‌دهی به معیارها یعنی تشخیص دهیم که اهمیت هر معیار به نسبتِ معیارهای دیگر چقدر است و بر این اساس ضریب یا وزن هر معیار را تعیین کنیم، مثلاً برای انتخاب یک خانه‌ی مسکونی مناسب می‌توانیم وزنِ معیارهای قیمت، سال ساخت و موقعیت جغرافیایی را به ترتیب ۴ و ۲ و ۱ تعیین کنیم، به این معنا که معیار “قیمت” چهار برابر از “موقعیت مکانی” و دو برابر از “سال ساخت” مهم‌تر است.

در این بخش از درس‌مان قصد داریم که با کمک تکنیک AHP، ضرایب یا وزن معیارها را محاسبه کنیم. برای انجام این کار، اولین شرط این است که معیارهایمان را در یک ساختار سلسله‌مراتبی (Hierarchy) قرار دهیم که شبیه آن را در درس درخت اهداف مشاهده کرده‌اید. به عبارتی، دقیقاً همان روشی که از درخت اهداف برای تجزیه‌ی اهداف کلّی‌تر به جزئی استفاده کردیم، در مورد معیارها نیز قابل استفاده است و می‌تواند آن‌ها را به صورت سلسله‌مراتبی مرتب کند. مثلاً اگر بخواهیم یک محصول رقابتی تولید کنیم و معیارهایمان کیفیت و قیمت باشند، با تجزیه‌ی آن‌ها به درخت زیر می‌رسیم:

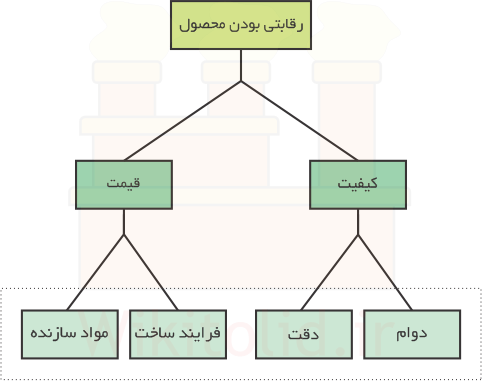
در استفاده از AHP برای تعیین وزن معیارها یا شناسایی گزینه‌های برتر، حتماً باید معیارهایی را انتخاب کنیم که در سطح یکسانی از درخت قرار گرفته‌ باشند. مثلاً مطابق نمودار بالا، برای مقایسه‌ی دو یا چند محصول از نظر رقابتی بودن، می‌توانیم آن‌ها را با معیارهای کیفیت و قیمت ارزیابی کنیم (هر دو در سطح دوم هستند) یا از معیارهای مواد سازنده، فرایند ساخت، دقت و دوام استفاده کنیم (همگی در سطح سوم هستند)، اما نباید از معیارهای قیمت، دوام و دقت استفاده کنیم چون در سطوح متفاوتی از نمودار قرار گرفته‌اند. البته روشن است که هر چقدر معیارها در سطوح پایین‌تری از نمودار قرار گرفته باشند از دقت و سادگی بیشتری برخوردارند و لذا معمولاً استفاده از آن‌ها در اولویت است.

پس از آن که معیارهای مورد نظر انتخاب شد، برای وزن‌دهی باید مراحل زیر را طی کنیم:

مرحله‌ی اول: ماتریس تصمیم‌گیری [C] را تشکیل می‌دهیم و عناصر آن را با مقایسه‌ی اهمیت معیارها تعیین می‌کنیم.

مرحله‌ی دوم: ماتریس [NormC] را تشکیل می‌دهیم و میانگین هر ردیف از آن را محاسبه می‌کنیم تا بردار {W} تعیین شود؛ عناصر این بردار وزن معیارها را نشان می‌دهند.

مرحله‌ی سوم: برای وزن‌های محاسبه شده آزمون سازگاری انجام می‌دهیم. اگر وزن‌ها سازگار باشند، کارمان به پایان می‌رسد و در غیر این صورت باید ماتریس [C] و مقایسه‌هایی که انجام داده‌ایم را اصلاح کنیم تا آزمون سازگاری به نتیجه برسد.

در ادامه جزئیات هر کدام این مراحل را با ذکر مثال بررسی می‌کنیم.

مرحله‌ی اول: تشکیل ماتریس تصمیم‌گیری یا ماتریس مقایسات زوجی یا [C]

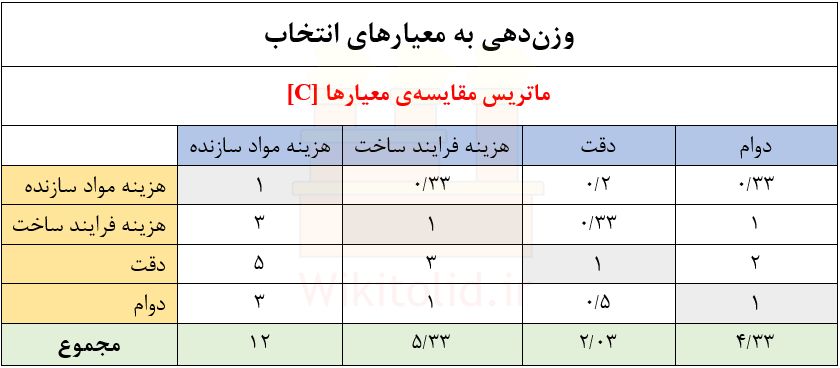
ماتریس [C] شبیه جدولی است که در آن معیارها را به صورت دو به دو از نظر میزان اهمیت مقایسه می‌کنیم، به همین علت گاهاً به آن ماتریس مقایسه‌ی زوجی یا ماتریس تصمیم‌گیری می‌گویند. در تصویر زیر می‌توانید نمونه‌ای از این ماتریس را مشاهده کنید. اگر تعداد معیارهایمان n عدد باشد، ماتریس [C] از نوع مربعی و با n ردیف و n ستون خواهد بود.

معیارها از چپ به راست به عنوان برچسب ستون‌ها (ردیف آبی) و از بالا به پایین به عنوان برچسب ردیف‌ها (ستون زرد) نوشته می‌شوند. سپس هر معیار در ردیف زرد از نظر میزان اهمیت با تمام معیارها در ردیف آبی مقایسه می‌شود و متناسب با آن نمره می‌گیرد. مثلاً ابتدا “هزینه‌ی مواد سازنده (در ستون زرد)” با “هزینه‌ی فرایند ساخت (در ردیف آبی)” مقایسه شده و نمره‌ی ۳۳% را گرفته است (یعنی اهمیت آن کمتر از هزینه‌ی فرایند ساخت است). بار دیگر “هزینه‌ی مواد سازنده” با “دقت” مقایسه شده و نمره‌ی آن آن ۲۰% ارزیابی شده است. همچنین هر معیار در مقایسه با خودش (مثلاً دوام با دوام، یا دقت با دقت) شرایط برابری دارد و طبیعتاً در خانه‌های خاکستری عدد ۱ قرار می‌گیرد.

از آن جایی که ممکن است جدول بالا با تصورتان از ماتریس متفاوت باشد، عناوین ردیف‌ها و ستون‌های آن را حذف کردیم. بدیهی است که جدول بالا هیچ تفاوتی با ماتریس زیر ندارد:

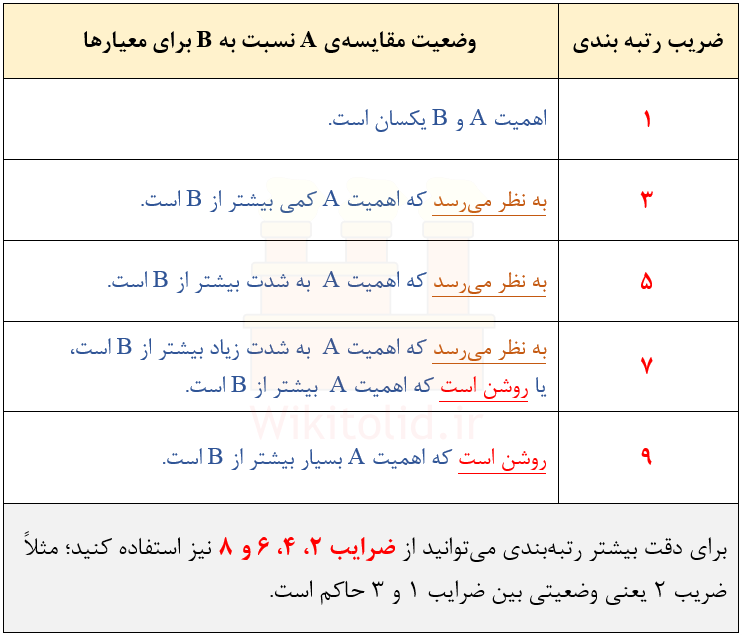
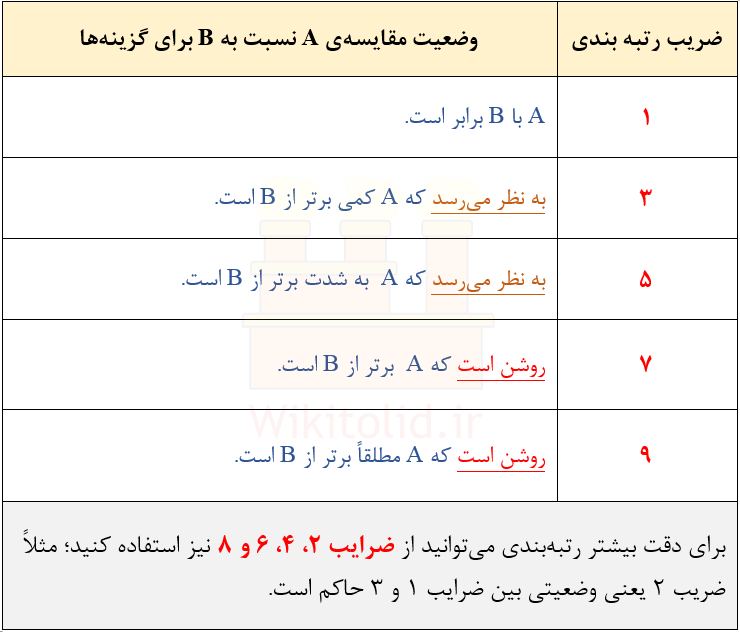
حال سؤال این است که آیا نمره‌ها سلیقه‌ای هستند یا از اصول خاصی پیروی می‌کنند؟ به عبارتی اعداد ۰٫۳۳ و ۰٫۲ و ۳ و ۵ در ماتریس [C] چگونه تعیین شده‌اند؟ در فرایند تحلیل سلسله ‌مراتبی (AHP) برای نمره دادن باید از استاندارد خاصی پیروی کنیم که در جدول زیر نشان داده‌ایم. مطابق این جدول، اگر اهمیت دو معیار یکسان باشد باید عدد یک را در ماتریس [C] منظور کنیم و به همین ترتیب، هر چقدر اهمیت معیار A  (عناوین ستون زرد) از معیار B (عناوین ردیف آبی) بیشتر باشد، نمره‌ی بالاتری منظور می‌گردد که حدأکثر آن ۹ است.

نکته‌ی مهمی که باید در نمره‌دهی رعایت شود این است که اگر در مقایسه‌ی پارامتر A با B نمره‌ی X را برای A در نظر گرفته ایم، در مقایسه‌ی B با A باید الزاماً نمره‌ی (۱/X) را برای B در نظر بگیریم، به همین علت است که در ماتریس بالا به اهمیت معیار “دقت” نسبت به “دوام” نمره‌ی ۲ داده‌ایم و به تبع آن اهمیت “دوام” نسبت به “دقت” برابر با ۰٫۵ شده است.

مرحله‌ی دوم: تشکیل ماتریس [NormC]

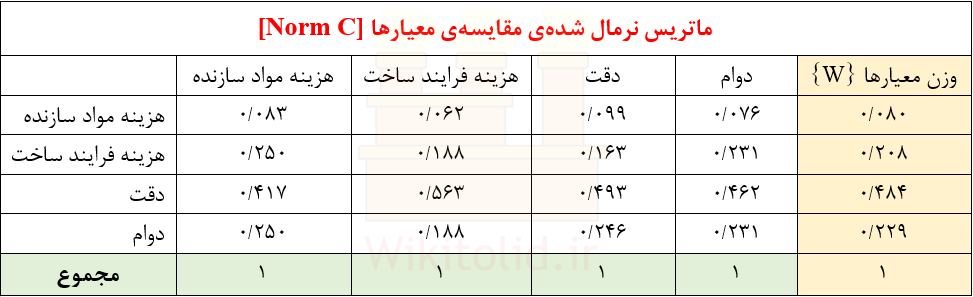
پس از کامل شدن ماتریس [C] اگر هر یک از عناصر آن را بر مجموع مقادیر ستونی که به آن تعلق دارد تقسیم کنیم، ماتریس [NormC] محاسبه می‌شود. مثلاً اولین عدد از اولین ستون ماتریس [C] در مرحله‌ی اول برابر با یک و مجموع مقادیر این ستون برابر ۱۲ بود، لذا عدد ۱ را بر ۱۲ تقسیم می‌کنیم و به عدد ۰٫۰۸۳ می‌رسیم که اولین ورودی از ماتریس [NormC] است.

پس از کامل شدن ماتریس [NormC] با محاسبه‌ی میانگین مقادیر در هر ردیف به اعدادی می‌رسیم که عناصر تشکیل دهنده‌ی بردار {W} هستند. این اعداد (عناصر بردار W) وزن‌هایی هستند که برای هر معیار محاسبه کرده‌ایم، مثلاً در ماتریس زیر، وزن معیار “هزینه‌ی مواد سازنده” برابر ۰٫۰۸۰  و وزن معیار “هزینه‌ی فرایند ساخت” برابر ۰٫۲۰۸ محاسبه شده است.

مرحله‌ی سوم: آزمون سازگاری

آزمون سازگاری کمک می‌کند تا از هماهنگی وزن‌های تعیین شده برای معیارها مطمئن شویم. معمولاً وقتی تعداد معیارها زیاد است، به سختی می‌توانیم هماهنگی وزن‌های شناسایی شده (بر اساس امتیازاتی که در ماتریس C داده‌ایم) را شناسایی کنیم و آزمون سازگاری برای کمک به این وضعیت طراحی شده است.

برای انجام آزمون سازگاری باید اقدامات زیر را انجام دهیم:

۱- بردار مجموع اوزان یا {Ws} را از ضرب ماتریس [C] در نمودار {W} محاسبه می‌کنیم.

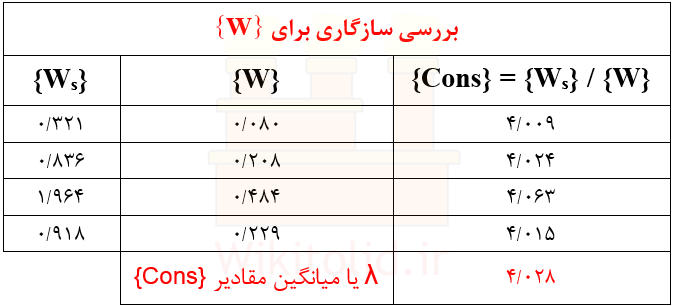
۲- بردار ثبات یا {Cons} را از تقسیم بردار {Ws} بر بردار {W}  محاسبه می‌کنیم.

۳- مقدار λ را با محاسبه‌ی میانگین مقادیر بردار {Cons} محاسبه می‌کنیم.

۴- شاخص هماهنگی یا CI را با کمک مقدار λ محاسبه می‌کنیم.

۵- نرخ هماهنگی یا CR را با کمک مقدار CI محاسبه می‌کنیم. اگر مقدار CR از ۰٫۱ کمتر باشد، هماهنگی وجود دارد.

اگر نتیجه‌ی آزمون سازگاری مثبت باشد الزاماً به معنای قابل اعتماد بودن وزن‌ها نیست، اما نشان می‌دهد که از نظر ریاضی منطقی به نظر می‌رسند. اگر نتیجه‌ی آزمون منفی باشد، هماهنگی وجود ندارد و لازم است تغییراتی در ماتریس [C] اعمال کنیم تا هماهنگی ایجاد شود.

مطابق مراحلی که گفتیم، در قدم اول باید بردار {Ws} را محاسبه کنیم:

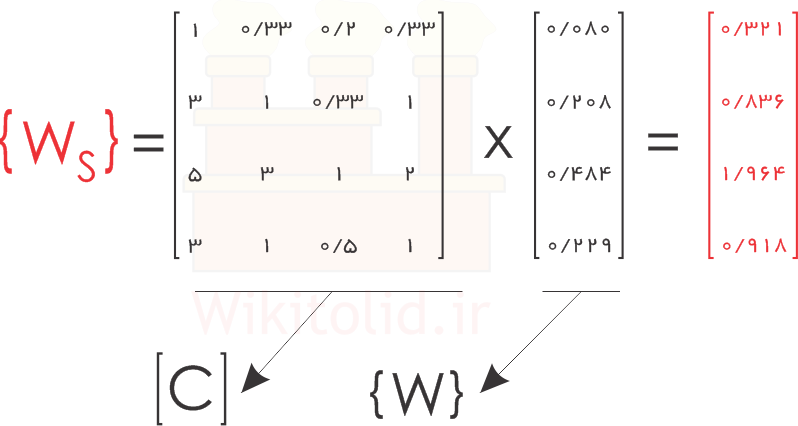
در ادامه با تقسیم مقادیر {Ws} بر {W}، بردار {Cons} را به دست می‌آوریم. با محاسبه‌ی میانگین مقادیر بردار {Cons} مقدار λ محاسبه می‌شود که برابر ۴٫۰۲۸  است.

برای محاسبه‌ی مقادیر CI‌ و CR باید از روابط زیر استفاده کنیم:

با داشتن λ و n (تعداد معیارها) مقدار CI محاسبه می‌شود که در مورد مثال‌مان برابر با ۰٫۰۸۲ است. برای محاسبه‌ی CR باید مقدار RI را داشته باشیم. RI مقداری است که بر اساس یک ماتریس تصادفی [C] به دست آمده و انتظار می‌رود که شاخص هماهنگی ما (CI) به مراتب از آن کمتر باشد. برای پیدا کردن مقادیر RI می‌توانید از جدول زیر استفاده کنید که بر اساس تعداد معیارها تنظیم شده‌اند. در مثال این درس چهار معیار داشتیم و لذا مقدار RI را ۰٫۸۹ در نظر می‌گیریم.

نهایتاً اگر مقدار CR از ۱/۰ کمتر باشد به این معناست که میان ضرایب انتخاب شده در ماتریس C هماهنگی وجود دارد، در غیر اینصورت نتیجه‌ی آزمون منفی است و باید تغییراتی در ماتریس [C] انجام دهیم تا هماهنگی بیشتری ایجاد شود و مقدار CR به کمتر از ۱/۰ برسد.

تعیین گزینه‌های برتر با کمک AHP

فرایند تحلیل سلسله ‌مراتبی  یا AHP می‌تواند برای انتخاب گزینه‌های برتر از میان چند گزینه مورد استفاده قرار بگیرد. به این منظور ابتدا باید معیارهای مورد نظرمان را انتخاب و وزن‌دهی کنیم که در بخش ابتدایی درس به آن پرداختیم، سپس باید اقدامات زیر را به ترتیب انجام دهیم.

مراحل اول تا سوم باید را به ازای هر معیار به صورت جداگانه انجام دهیم:

۱- ماتریس [C] را برای مقایسه‌ی گزینه‌ها نسبت به معیار مورد نظر تشکیل می‌دهیم. (قبلاً این کار را برای مقایسه و وزن‌دهی معیارها انجام داده بودیم)

۲- ماتریس [NormC] و بردار اولویت‌بندی {P_i} را تشکیل می‌دهیم؛ حرف i شماره‌ی هر معیار است، مثلاً P₁ اولویت‌بندی گزینه‌ها نسبت به معیار شماره‌ی یک را نشان می‌دهد.

۳- آزمون سازگاری را انجام می‌دهیم.

وقتی سه مرحله‌ی بالا را جداگانه برای تمام معیارها انجام دادیم، نوبت به اقدامات زیر می‌رسد:

۴- ماتریس رتبه‌بندی نهایی [FRating] را تشکیل می‌دهیم.

۵- ارزش (Value) هر گزینه را با ترانهاده کردن ماتریس [FRating] و ضرب آن در بردار {W} به دست می‌آوریم.

در ادامه هر یک از مراحل بالا را با ذکر مثال تشریح می‌کنیم.

مراحل اول تا سوم (جداگانه برای هر معیار)

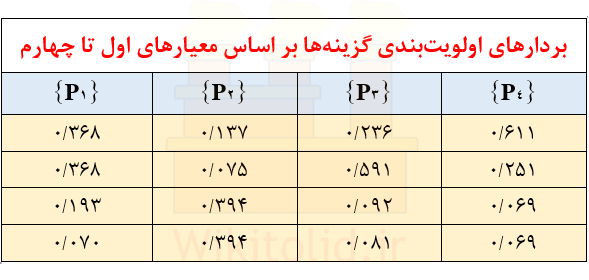
همانطور که گفتیم این مراحل باید برای هر معیار به صورت جداگانه انجام شود، مثلاً در مثال این درس چهار معیار داشتیم و در نتیجه مراحل اول تا سوم باید چهار بار برای آن‌ها تکرار شود. اگر معیارها را شماره‌گذاری کنیم، نهایتاً با پایان مرحله‌ی سوم، بردار اولویت‌بندی یا {P_i} به دست می‌آید که i شماره‌ی آن معیار را نشان می‌دهد. روشن است که وقتی چهار معیار داریم، قبل از ورود به مرحله‌ی چهارم و با تکرار این سه مرحله، باید بردارهای P₁، P₂، P₃ و P₄ را به دست آورده باشیم.

 در ادامه، این سه مرحله را فقط یک بار برای معیار “هزینه‌ی مواد اولیه” انجام می‌دهیم تا بردار {P₁} محاسبه شود.

مرحله‌ی اول: تشکیل ماتریس [C]

برای تشکیل ماتریس [C] دقیقاً مشابه کاری که در بخش اول درس انجام دادیم، ابتدا گزینه‌ها را به عنوان برچسب ستون‌ها و ردیف‌ها می‌نویسیم و سپس ورودی‌های ماتریس را با مقایسه‌ی دو به دوی گزینه‌ها نسبت به معیار مورد نظرمان تکمیل می‌کنیم. همان استانداردی که در بخش اول برای نمره‌دهی رعایت کردیم، در این بخش هم قابل استفاده است:

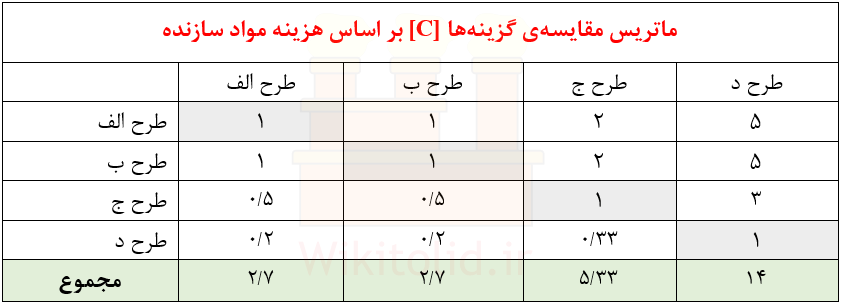
با توجه به جدول بالا و پس از مقایسه‌ی دو به دوی گزینه‌ها، ماتریس [C] را تشکیل می‌دهیم:

مرحله‌ی دوم: تشکیل [NormC] و به دست آوردن {P_i}

 

اگر هر عنصر از ماتریس [C] را در مجموع مقادیر ستونی که در آن قرار گرفته تقسیم کنیم، ماتریس [NormC]  به دست می‌آید. با محاسبه‌ی میانگین هر ردیف از [NormC] عناصر بردار {P₁} به دست می‌آیند که آن‌ها را با پس ‌زمینه‌ی نارنجی نشان دادیم. یادآوری می‌کنیم که قبلاً در بخش اول، از محاسبه‌ی میانگین هر ردیف از ماتریس [NormC] بردار {W} را به دست آورده بودیم که وزن معیارها را نشان می‌داد.

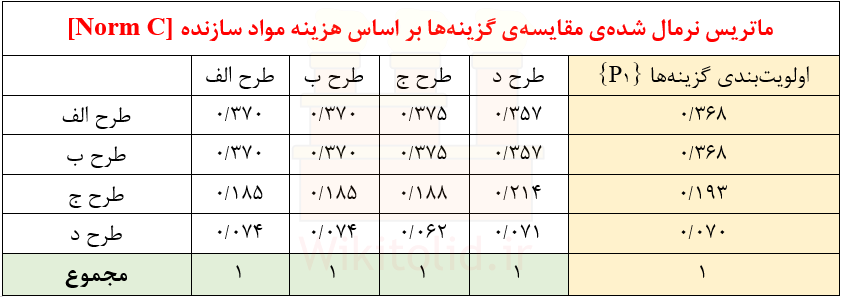
مرحله‌ی سوم: انجام آزمون هماهنگی

آزمون هماهنگی دقیقاً مشابه اقداماتی که در بخش اول انجام دادیم، به این ترتیب انجام می‌شود که ابتدا بردار {P_S} را با ضرب ماتریس [C] در {P₁} به دست می‌آوریم. سپس مقادیر λ و CI و CR را محاسبه می‌کنیم و نهایتاً اگر مقدار CR‌ کمتر از ۰٫۱ شود به معنای هماهنگی عناصر در ماتریس [C] است. در مثال بالا، مقدار CR برابر ۰٫۰۰۶  محاسبه شده که بسیار کمتر از ۰٫۱ است و هماهنگی میان عناصر را نشان می‌دهد.

مراحل چهارم و پنجم

بعد از انجام مراحل اول تا سوم برای تمام معیارها و تشکیل بردارهای اولویت‌بندی {Pi} برای آن‌ها، می‌توانیم ارزش گزینه‌ها را با انجام مراحل چهارم و پنجم محاسبه کنیم؛ نهایتاً گزینه‌‌ای که ارزش آن بیشتر از سایر گزینه‌ها محاسبه شده است در اولویت انتخاب قرار می‌گیرد.

با توجه به اینکه در مراحل اول تا سوم فقط بردار {P₁} را محاسبه کردیم، فرض کنید بردارهای {P₂} و {P₃} و {P₄} مطابق زیر هستند:

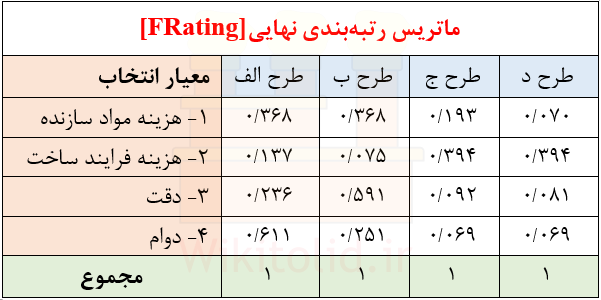
مرحله چهارم: تشکیل ماتریس رتبه‌بندی نهایی [FRating]

تعداد ردیف‌های ماتریس [FRating] برابر با تعداد معیارها است و عناصر ردیف اول آن شامل عناصر بردار {P₁} و عناصر ردیف دوم آن شامل عناصر بردار {p₂} و به همین ترتیب عناصر ردیف i آن شامل عناصر بردار {P_i} است. مثلاً در مثالی که برای این درس ارائه کردیم، ردیف اول ماتریس [FRating] شامل عناصر {P1} یا  ۰٫۳۶۸ و ۰٫۳۶۸ و ۰٫۱۹۳ و ۰٫۰۷۰ است.

مرحله پنجم: محاسبه‌ی ارزش گزینه‌ها

در مرحله‌ی پنجم باید ارزش گزینه‌ها (Alternative Value) را با رابطه‌ی زیر محاسبه کنیم:

ماتریس [F Rating] را در مرحله‌ی چهارم محاسبه کردیم اما در مرحله‌ی پنجم به ترانهاده‌ی آن نیاز داریم. یادآوری می‌کنیم که ترانهاده‌ی یک ماتریس به صورت زیر به دست می‌آید:

لذا ترانهاده‌ی [F Rating] عبارت است از:

بردار {W} یا وزن‌های اختصاص یافته به معیارها را در بخش اول درس (مربوط به تعیین وزن معیارها با AHP) محاسبه کردیم. در ادامه داریم: