شما در حال خواندن درس شاخصهایی برای اندازهگیری دقت پیشبینی از مجموعه پیشبینی تقاضا هستید.
تصمیمهای ما برای آینده هستند. محصولی که امروز طراحی میکنیم، شاید سالها بعد عرضه شود. سولهها و تجهیزاتی که امروز میخریم، باید به نیازهای آیندهمان پاسخ دهند. برای همین میتوانیم ادعا کنیم که: پیشبینی آینده از لازمههای مدیریت است. با این وجود، آینده نامعلوم است و نتایج پیشبینی ممکن است فاصلهی زیادی با حقایق آینده داشته باشند. برای همین حتیالمقدور باید شناسایی کنیم که کدام پیشبینیها دقیقتر و کدام فاقد دقت کافی هستند.
یکی از سادهترین راهها برای سنجش دقت پیشبینی، استفاده از شاخصها است. شاخصها با استفاده از روابط ریاضی، خطای پیشبینی را اندازهگیری میکنند. در این درس با چند شاخص مهم شامل: میانگین انحراف مطلق (MAD)، میانگین مجذور خطاها (MSE)، میانگین درصد خطای مطلق (MAPE) و انحراف معیار (SD) آشنا خواهید شد.
ممکن است به ذهن برسد: چه فایده دارد که وقتی آینده اتفاق افتاد، دقت پیشبینیهای گذشته را بسنجیم؟ این کار مفید است، زیرا به ارتقای مدلها و روشهای پیشبینی کمک میکند. مثلاً اگر ببینیم روشی که تا به امروز برای پیشبینی استفاده میکردیم، قابل اعتماد نیست و دقت کافی ندارد، روش دیگری را جایگزین آن میکنیم. اما ناگفته نماند که برای استفاده از شاخصها و سنجش دقت پیشبینی، لازم نیست منتظر آینده بمانیم؛ بلکه میتوانیم با همان روشی که قرار است آینده را پیشبینی کنیم، دورههای قبلی را تخمین بزنیم تا ببینیم نتایج آن چقدر با واقعیت همخوانی دارد.
مقدمهای برای درک بهتر درس:
روش محاسبه مجموع خطای پیشبینی
پیش از آشنایی با شاخصها، مناسب است با روش جمع زدن مقادیر خطا آشنا باشیم. خیلی اوقات، پیشبینی برای چند دورهی مختلف انجام شده و میخواهیم ببینیم مقدار کلی خطا چقدر بوده است. در این موارد، میتوانیم میانگین خطا در دورههای مختلف را محاسبه کنیم.
برای محاسبه میانگین خطا، باید مجموع مقادیر خطا را به دست آورده و بر تعداد دورهها تقسیم کنیم. مثلاً فرض کنید مقدار تقاضا را برای دوازده ماه سال پیشبینی کردهایم. شاید پیشبینی ما این بوده که تقاضا در بهمن به ۱۲۰ واحد میرسد، اما به ۱۰۰ واحد رسیده باشد. این ۲۰ واحد، خطای پیشبینی برای بهمن است. اما اگر بخواهیم میانگین خطای پیشبینی برای دوازده ما را حساب کنیم، باید مقادیر خطای همه ماهها را جمع بزنیم و بر عدد ۱۲ تقسیم کنیم. اما چگونه مقادیر را جمع بزنیم؟ آیا باید مثبت یا منفی بودن مقادیر را لحاظ کنیم یا همه آنها را مثبت فرض کنیم؟ پاسخ کوتاه این است که حسب مورد، هر دو مورد ممکن است مفید باشند.
اگر همه مقادیر خطا را مثبت فرض کنیم، ارزش مطلق مقادیر خطا یا Absolute Value of the Error به دست میآید. اما اگر علامت مقادیر -مثبت یا منفی بودن- را لحاظ کنیم، خطای تجمعی یا Cumulative Sum of Errors به دست میآید که CFE یا RSFE یا Running Sum of Forecast Errors نیز نام دارد.
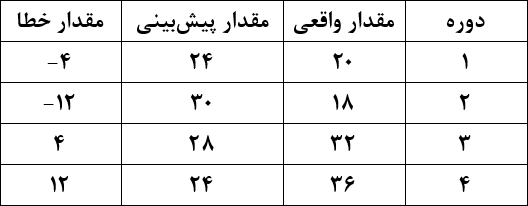
در جدول زیر، خطای تجمعی برابر صفر است. تصور کنید در جدولی مثل زیر که مقادیر خطا نسبت به مقادیر واقعی قابل توجه است، مجموع خطا را صفر اعلام کنیم. این میتواند گمراهکننده باشد، برای همین خیلی اوقات خطای تجمعی قابل قبول نیست، چرا که مقادیر مثبت و منفی یکدیگر را حنثی میکنند. اما گاهی از خطای تجمعی برای کنترل فرایند پیشبینی استفاده میشود؛ اگر مقدار خطای تجمعی نزدیک صفر باشد، نشان میدهد که نتایج به سمت مثبت یا منفی منحرف نشدهاند و اگر خطایی هست، مقادیر مثبت و منفی یکدیگر را خنثی کردهاند. اما اگر مقدار خطای تجمعی به سمت مثبت یا منفی تشدید شود، نشان از منحرف شدن نتایج به یک سمت خاص دارد و شاید لازم باشد برای اصلاح مدل پیشبینی چارهاندیشی کنیم.
میانگین انحراف مطلق
(Mean Absolute Deviation یا MAD)
برای محاسبه شاخص MAD، همه مقادیر خطا را مثبت فرض کرده و از آنها میانگین میگیریم. بنابراین اگر تقاضای واقعی برابر ۱۰ واحد باشد، فرقی نمیکند که تقاضای پیشبینی شده ۸ واحد یا ۱۲ واحد بوده باشد، زیرا در هر دو حالت مقدار خطا را ۲+ واحد (نه ۲+ واحد یا ۲− واحد) اعلام میکنیم. شاخص MAD از رابطه زیر به دست میآید:

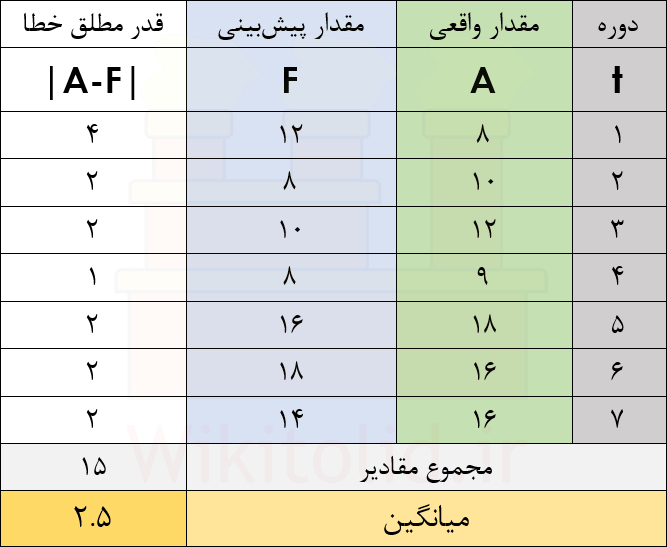
در جدول زیر، جای این که مقادیر واقعی خطا را لحاظ کنیم، قدر مطلق یا مقدار مثبت آنها را در نظر گرفتهایم. سپس از مقادیر قدر مطلق خطا میانگین گرفته و شاخص MAD را ۲.۵ به دست آوردهایم.
میانگین مجذور مقادیر خطا
(Mean of Squared Error)
برای محاسبه این شاخص، مقدار خطا در هر دوره را به توان دو میرسانیم. وقتی مقداری به توان دو میرسد، علامت آن در هر صورت مثبت است، برای همین فرقی نمیکند که مقدار خطای واقعی مثبت یا منفی باشد. همچنین به توان دو رسیدن مقادیر خطا باعث میشود که این شاخص، حساسیت بیشتری نسبت به مقادیر خطا داشته باشد؛ پس در جایی از آن استفاده میکنیم که بخواهیم نظارت یا کنترل دقیقتری روی مقادیر خطا داشته باشیم.

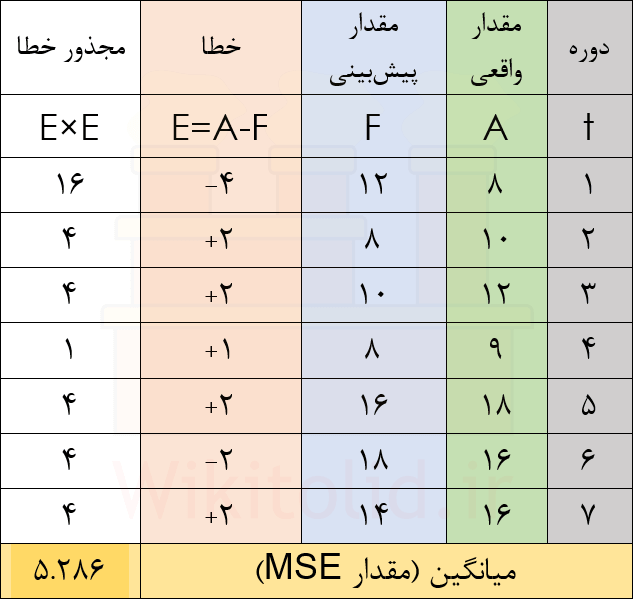
در جدول زیر، شاخص MSE را ۵.۲۸۶ محاسبه کردهایم.
میانگین درصد خطای مطلق
(Mean of Absolute Percent Error)
برای محاسبه شاخص MAPE، خطای پیشبینی در هر دوره را بر مقدار واقعی تقسیم میکنیم. مثلاً اگر پیشبینی کرده بودیم که تقاضا در بهمن به ۱۰ واحد میرسد اما به ۸ واحد رسیده باشد، یعنی ۲ واحد خطا داشتهایم. عدد ۲ را بر ۸ تقسیم میکنیم و متوجه میشویم خطای ما ۲۵ درصد مقدار تقاضای واقعی بوده است. در این جا کاری به مثبت یا منفی بودن مقادیر خطا نداریم و همه را مثبت در نظر میگیریم. همین محاسبات را برای همه دورهها انجام میدهیم. در پایان از این مقادیر میانگین میگیریم تا مقدار شاخص MAPE مشخص شود.

شاخص MAPE به واحد اندازهگیری وابسته نیست، برای همین ابزار مناسبی برای مقایسه است. مثلاً فرض کنید مقدار فروش در یک کارخانه را به شکل زیر پیشبینی کردهایم.
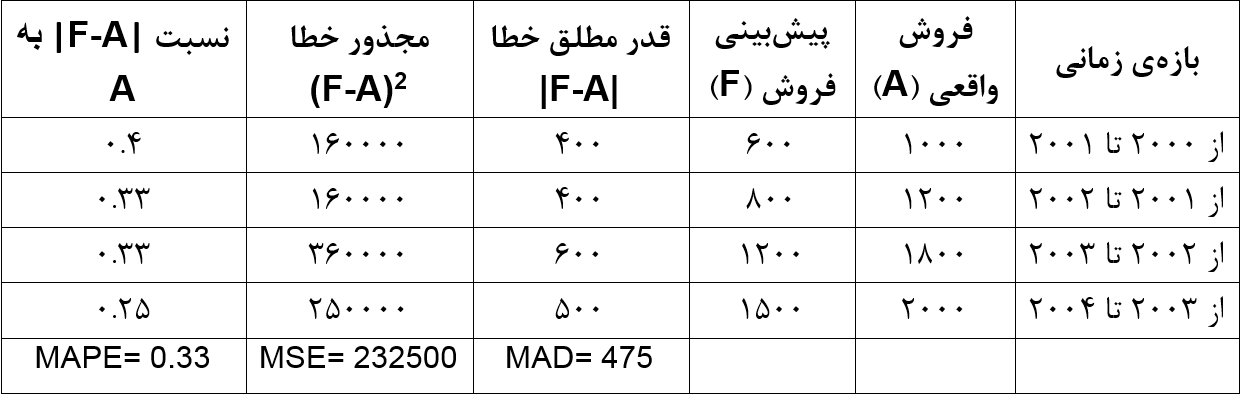
همچنین مقدار سود را به شکل زیر پیشبینی کردهایم.
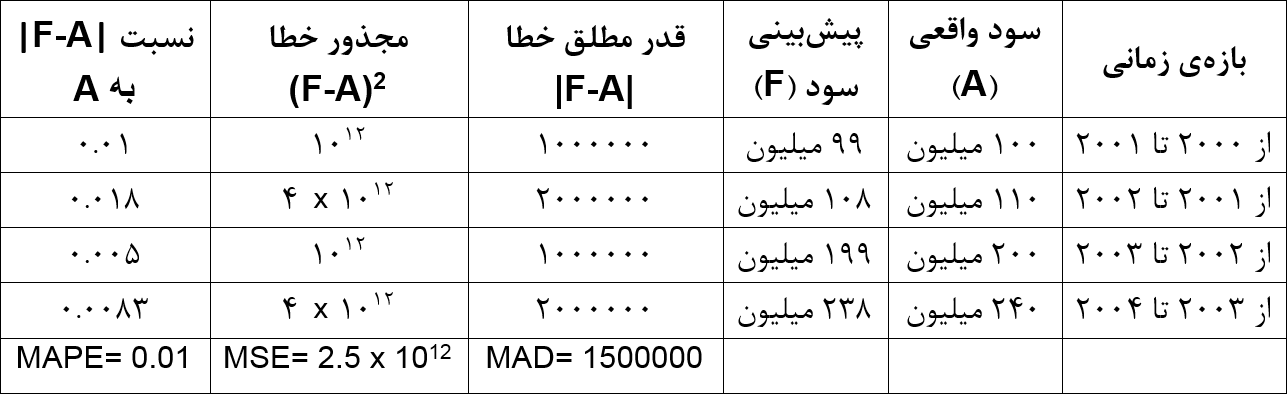
کدام پیشبینی دقیقتر است؟ اگر MAD را لحاظ کنیم، میانگین قدر مطلق خطا در پیشبینی اول ۴۷۵ و در پیشبینی دوم ۱۵۰۰۰۰۰ است، اما این مقایسه درست نیست. واحد اندازهگیری در پیشبینی اول «تعداد محصول» و در پیشبینی دوم «تومان» است. اما شاخص MAPE درصد خطا را نشان میدهد و کاری به واحد اندازهگیری ندارد. بر اساس شاخص MAPE، خطای پیشبینی اول ۳۳% و خطای پیشبینی دوم ۱% به دست میآید، بنابراین پیشبینی دوم دقیقتر از پیشبینی اول است.
انحراف معیار
(Standard Deviation)
شاخص انحراف معیار، برای سنجش پراکندگی دادهها است. با کمک این شاخص متوجه میشویم که خطای پیشبینی هر دوره چقدر به خطای میانگین نزدیک است. اگر انحراف از معیار کم باشد، یعنی پیشبینیها یکواخت هستند. این شاخص را با رابطه زیر محاسبه میکنیم:

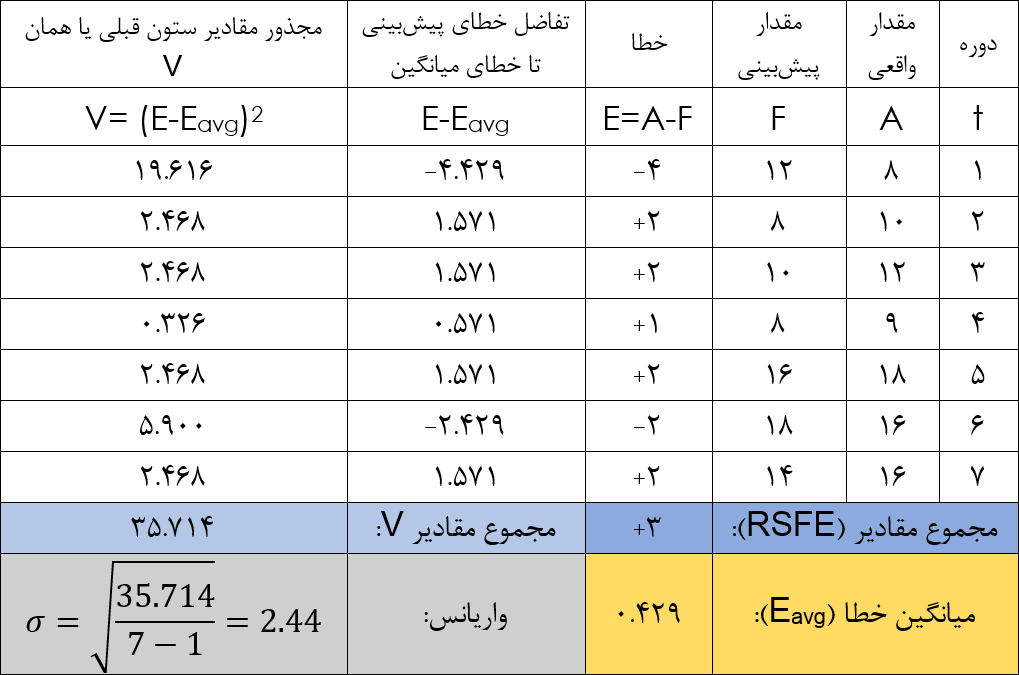
برای محاسبهی انحراف معیار: مقدار خطای میانگین را محاسبه میکنیم (Eavg). سپس مشخص میکنیم که خطای پیشبینی در هر دوره (t) چقدر از میانگین فاصله داشته و آن را به توان دو میرسانیم. مجموع این مقادیر را محاسبه کرده و بر n-1 تقسیم میکنیم. n تعداد دورهها است. از عددی که به دست آمده جذر میگیریم تا انحراف معیار را محاسبه کنیم.

دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.