شما در حال خواندن درس مدل EOQ با پشتیبانی از تخفیف کلی از مجموعه مدیریت موجودی هستید.
در نسخه ساده مدل EOQ یکی از فرضها این است که: «هزینه خرید هر واحد موجودی ثابت میماند». در این درس میخواهیم این فرض را به چالش کشیده و مدل EOQ را طوری توسعه دهیم که از «تخفیف در ازای خرید بیشتر» پشتیبانی کند. در این حالت هزینه خرید ثابت نمیماند، بلکه ممکن است با تغییر دادن مقدار سفارش تغییر کند. مثلاً شاید قیمت خرید محصول برای سفارش با مقدار کمتر از ۱۰۰ واحد برابر ۲۰۰۰ تومان و برای سفارش بیشتر از ۱۰۰ واحد برابر ۱۸۰۰ تومان باشد.
تخفیفها ممکن است روی کل سبد خرید یا روی بخشی از آن اعمال شوند. مدلی که در این درس ارائه خواهیم کرد، با این فرض است که تخفیفها روی کل سبد خرید اعمال میشوند. مثلاً فرض کنید فروشنده اعلام کند قیمت محصول برای سفارشات بالای ۱۰۰ واحد برابر ۱۸۰۰ تومان و برای سفارشات کمتر برابر ۲۰۰۰ تومان است. فرض ما این است که اگر ۱۲۰ واحد از محصول را سفارش دهیم، تخفیف روی تمام این ۱۲۰ واحد اعمال میشود. اما بر خلاف این فرض شاید منظور فروشنده این باشد که وقتی ۱۲۰ واحد از محصول را سفارش میدهیم، قیمت ۱۰۰ واحد اول ۲۰۰۰ تومان و قیمت ۲۰ واحد دوم ۱۸۰۰ تومان است.
توسعه مدل EOQ برای پشتیبانی از تخفیف روی همه محصولات
با در نظر داشتن فرضی که راجع به کلی بودن تخفیفها گفتیم، قیمتهای اعلام شده توسط فروشنده را میتوانیم در جدولی مثل زیر درج کنیم. در این جدول فقط به سه قیمت اشاره شده است، حال آن که شاید فروشنده قیمتهای بیشتر یا کمتری اعلام کند؛ مدلی که در این درس ارائه خواهیم کرد محدودیتی در مورد تعداد قیمتهای اعلام شده ندارد.
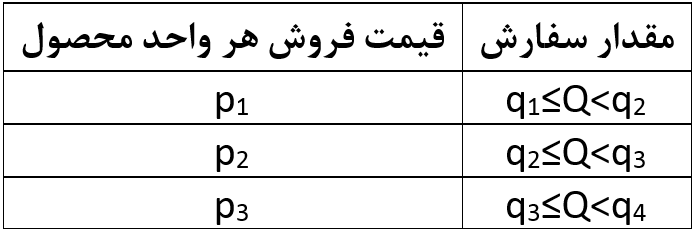
به طور کلی وقتی فروشنده m قیمت مختلف اعلام میکند، مقدار سفارشات مربوط به هر بازه را میتوانیم به شکل qi≤Q˂qi+1 و قیمت اعلام شده برای هر بازه را میتوانیم به شکل pi نشان دهیم؛ با این توضیح که i میتواند هر عدد صحیحی از ۱ تا m باشد.
در درس مدل EOQ توضیح دادیم که مجموع هزینههای موجودی از رابطه زیر به دست میآید.
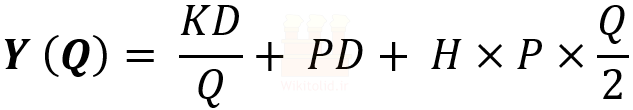
در این درس بر خلاف شکل ساده مدل EOQ، قیمت (P) ثابت نیست و بر اساس مقدار سفارش تغییر میکند؛ لذا بر اساس قیمتهای مختلف باید چند تابع هزینه مختلف بنویسیم. مثلاً اگر سه قیمت مختلف داشته باشیم، باید سه تابع هزینه مختلف تشکیل دهیم. این وضعیت را میتوانیم با رابطه زیر نمایش دهیم، با این توضیح که i میتواند از ۱ تا m باشد و m تعداد قیمتهای اعلام شده است.
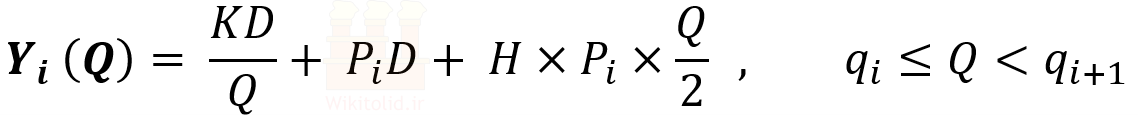
فرض کنید سه قیمت مختلف از سوی تامینکننده اعلام شده باشد، در این حالت بر اساس هر قیمت یک تابع هزینه داریم و اگر آنها را رسم کنیم، نموداری شبیه زیر به دست میآید.
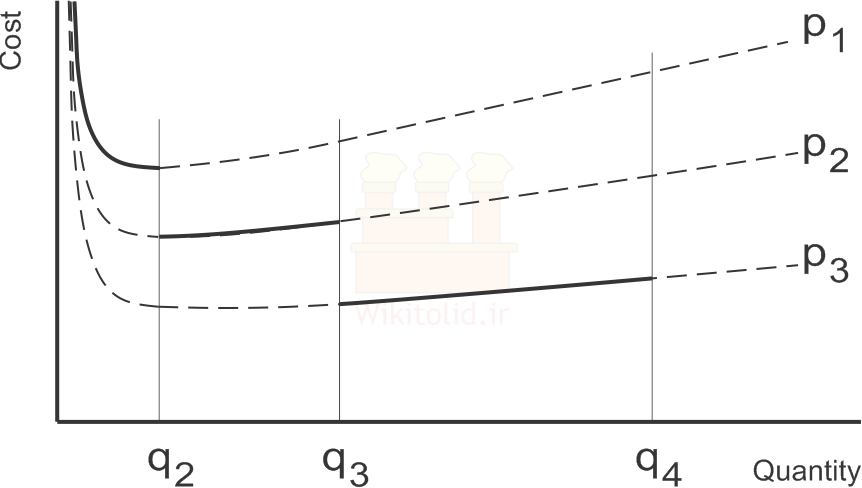
در همه این نمودارها: اگر مقدار سفارش بسیار کم باشد، هزینه موجودی بسیار بالا خواهد بود؛ اما همانطور که آرام آرام مقدار سفارش بزرگتر میشود، مجموع هزینههای موجودی با شیب زیاد کاهش مییابد. این روند کاهشی ادامه دارد تا جایی که دیگر افزایش مقدار سفارش باعث کاهش هزینه نمیشود، بلکه اتفاقاً آن را افزایش میدهد. بر این اساس میتوانیم اقتصادیترین مقدار سفارش را با کمک الگوریتم زیر پیدا کنیم:
گام اول- ابتدا تلاش میکنیم مقدار اقتصادی سفارش را روی آخرین منحنی بیابیم. در آخرین منحنی، قیمت پایینتر از منحنیهای دیگر است و احتمال این که بتوانیم نقطه مطلوب را بیابیم بیشتر است. البته میدانیم که خیلی اوقات هزینههای نگهداری باعث میشوند که خرید محصول در مقدار زیاد توجیهپذیر نباشد؛ پس شاید بهترین مقدار سفارش روی منحنی دیگری قرار بگیرد.
گفتیم m تعداد قیمتهای اعلام شده و البته تعداد بازههای تعیین شده برای سفارشات است. کمترین قیمت اعلام شده برای وقتی است که مقدار سفارش در بازه qm≤Q˂qm+1 باشد؛ در این بازه قیمت خرید هر واحد محصول Pm است و مقدار اقتصادی سفارش از رابطه زیر محاسبه میشود:
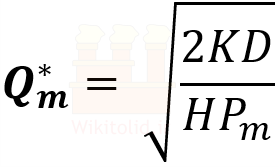
در ارتباط با حاصل معادله بالا دو حالت قابل تصور است:
۱- اگر حاصل رابطه بالا در بازه qm≤Q˂qm+1 باشد، مسأله حل شده است و بهترین مقدار برای سفارش را یافتهایم.
۲- اگر حاصل رابطه بالا خارج از بازه qm≤Q˂qm+1 باشد، مقدار به دست آمده روی آخرین منحنی قرار نمیگیرد و نمیتوانیم محصول را با قیمت Pm خریداری کنیم؛ لذا این مقدار را کنار گذاشته و فعلاً برای گام اول فرض میکنیم که بهترین مقدار سفارش برابر qm است. این فرض بر اساس نموداری است که بالاتر دیدیم؛ چرا که معمولاً انتظار میرود در همه منحنیها به جز منحنی اول، هر چه مقدار سفارش افزایش مییابد، هزینههای موجودی نیز افزایش یابد؛ البته این به شرطی است که روند نزولی نمودار به پایان رسیده و رشد مثبت آن آغاز شده باشد، اما معمولاً بازههای تعریف شده به نحوی هستند که این اتفاق در همه منحنیها به جز منحنی اول دیده میشود. بنابراین تا این لحظه مقدار بهینه سفارش را qm فرض میکنیم.
![]()
تابع Ym در واقع همان تابع مجموع هزینهها در حالتی است که هزینه خرید هر واحد محصول برابر Pm باشد؛ به عبارتی این تابع، هزینههای موجودی روی آخرین منحنی (یا منحنی شماره m) را نشان میدهد. فرض کردیم بهینهترین مقدار سفارش برابر Qm است، پس این مقدار را در تابع هزینه وارد میکنیم تا ببینیم با این فرض، مجموع هزینههای موجودی چقدر خواهد بود. سپس گام دوم را شروع میکنیم.
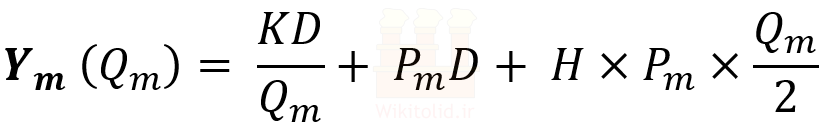
گام دوم- اگر کار در گام اول تمام نشده باشد، برای ادامه بررسی از منحنی آخر عبور کرده و یک منحنی قبل از آن را بررسی میکنیم. پس مقدار i را یک واحد کم میکنیم و مقدار جدید هزینه خرید را در معادله زیر قرار میدهیم. برای مثال اگر سه قیمت اعلام شده باشد و قبلاً منحنی سوم را بررسی کرده باشیم، حالا i را برابر دو قرار میدهیم و منحنی دوم را بررسی میکنیم.
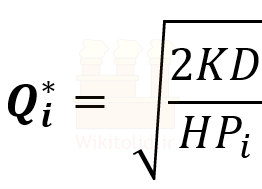
در ارتباط با حاصل رابطه بالا دو حالت قابل تصور است:
۱- اگر حاصل رابطه بالا در بازه مربوط به منحنی مورد نظر باشد، آن را در تایع هزینه قرار میدهیم تا ببینیم مجموع هزینههای موجودی چقدر میشود.
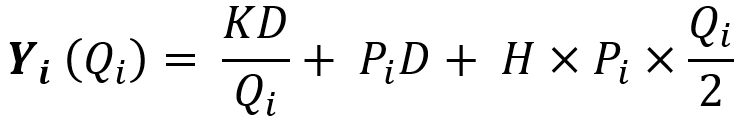
اگر هزینه به دست آمده کمتر از هزینه حداقلی باشد که آخرین بار به دست آوردیم، مقدار مناسبتری برای Q پیدا کردهایم و مساله حل شده است. در غیر این صورت فرض میکنیم آخرین مقدار بهینهای که قبلاً برای Q محاسبه کردیم، اقتصادیترین مقدار سفارش است و حل مسأله به پایان میرسد.
۲- اگر حاصل رابطه بالا در بازه مورد نظر نباشد، به ابتدای بازه میرویم و Q را برابر qi قرار میدهیم. سپس بررسی میکنیم که در این حالت هزینههای موجودی چقدر است؟ اگر این هزینه کمتر از مقداری باشد که قبلاً به عنوان کمترین هزینه موجودی یافتهایم، مقدار qi را جایگزین مقدار قبلی میکنیم. اما اگر مقدار جدید نسبت به قبل هزینههای بیشتری داشته باشد، گزینه مناسبی نیست و دو راه باقی میماند:
اگر هنوز منحنی دیگری برای بررسی باقی مانده باشد، مرحله دوم را برای آن تکرار میکنیم.
اگر منحنی دیگری نمانده باشد، بهترین مقدار سفارشی که تا این لحظه یافتهایم را به عنوان پاسخ نهایی اعلام میکنیم.
مثال اول
فرض کنید تقاضای سالیانه برای موجودی ۷۲۰۰ واحد (D=720)، هزینه ثابت سفارش برای هر واحد موجودی برابر ۲۰۰ تومان (K=200) و هزینه نگهداری از هر واحد محصول سالیانه ۱۰% قیمت خرید (H=0.1) باشد. همچنین هزینه خرید موجودی نسبت به مقدار سفارش بر اساس جدول زیر تعیین میشود:

گام اول برای یافتن بهترین نقطه سفارش در بازه سوم: جستجو برای مقدار اقتصادی سفارش را از بازه سوم شروع میکنیم. در این بازه قیمت برابر ۱۸ تومان است و مقدار بهینه سفارش از رابطه زیر به دست میآید:
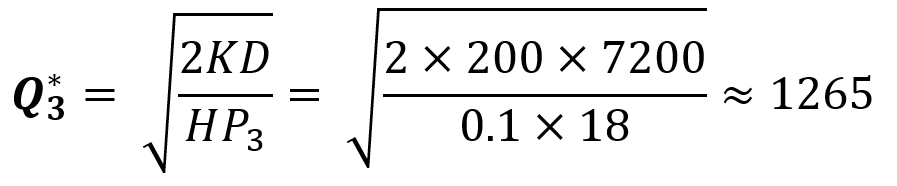
مقدار اقتصادی برابر ۱۲۶۵ واحد به دست آمده است. این یک مقدار منطقی است و در بازه منحنی سوم قرار دارد، پس آن را پذیرفته و به عنوان اقتصادیترین مقدار سفارش در نظر میگیریم.
مثال دوم
فرض کنید تقاضای سالیانه برای موجودی ۴۰۰۰ واحد (D=4000)، هزینه ثابت سفارش برای هر واحد موجودی برابر ۴۰۰ تومان (K=400) و هزینه نگهداری از هر واحد محصول سالیانه ۴۰% قیمت خرید (h=0.4) باشد. همچنین هزینه خرید موجودی نسبت به مقدار سفارش بر اساس جدول زیر تعیین میشود:

گام اول برای یافتن بهترین نقطه سفارش در بازه سوم: جستجوی مقدار بهینه سفارش را از بازه سوم شروع میکنیم. در این بازه قیمت برابر ۱۹۲ تومان است و مقدار بهینه سفارش از رابطه زیر به دست میآید:
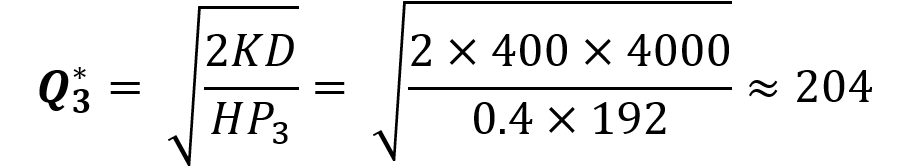
مقدار اقتصادی برابر ۲۰۴ واحد به دست آمده، اما زمانی میتوانیم محصول را با قیمت ۱۹۲ تومان خریداری کنیم که سفارش بالای ۱۲۰۰ واحد باشد، پس این نتیجه قابل استفاده نیست. مطابق توضیحاتی که دادیم، کمترین هزینه مربوط به ابتدای هر بازه است، پس فعلاً فرض میکنیم بهترین مقدار سفارش برابر ۱۲۰۰ واحد باشد. اگر قیمت هر واحد محصول ۱۹۲ تومان و مقدار سفارش ۱۲۰۰ واحد باشد، هزینههای موجودی برابر است با:
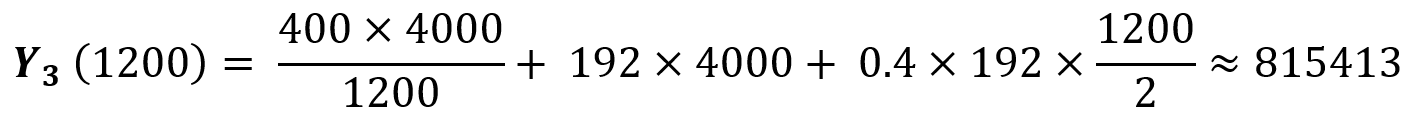
گام دوم برای یافتن بهترین مقدار سفارش در بازه دوم: منحنی دوم را بررسی میکنیم. در این بازه قیمت برابر ۱۹۸ تومان است و مقدار بهینه سفارش از رابطه زیر به دست میآید:
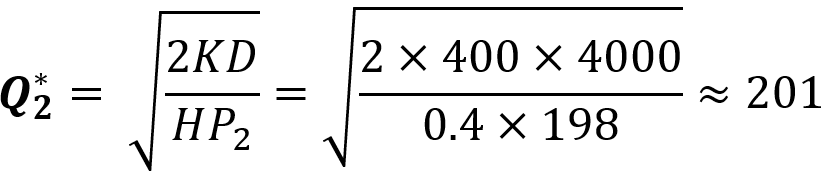
این مقدار در بازه منحنی دوم نیست. کمترین هزینه در منحنی دوم مربوط به شروع آن یا مقدار سفارش برابر با ۴۰۰ واحد است. در این حالت هزینههای موجودی برابر است با:
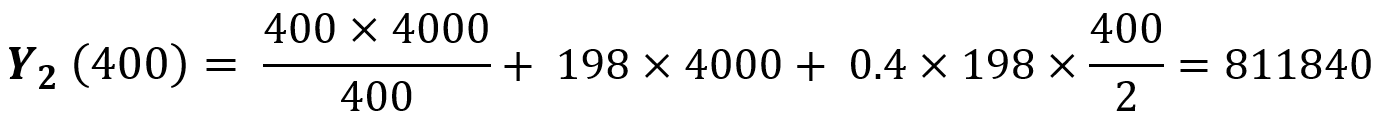
اگر مقدار سفارش ۴۰۰ واحد باشد، مجموع هزینههای موجودی برابر ۸۱۱۸۴۰ است؛ این هزینه کمتر از وقتی است که سفارش را با مقدار ۱۲۰۰ واحد ثبت میکنیم. در نتیجه مقدار اقتصادی سفارش را ۴۰۰ واحد در نظر گرفته و منحنی اول را بررسی میکنیم.
تکرار گام دوم برای یافتن بهترین مقدار سفارش در بازه اول: در این بازه قیمت برابر ۲۰۰ تومان است و مقدار بهینه سفارش از رابطه زیر به دست میآید:
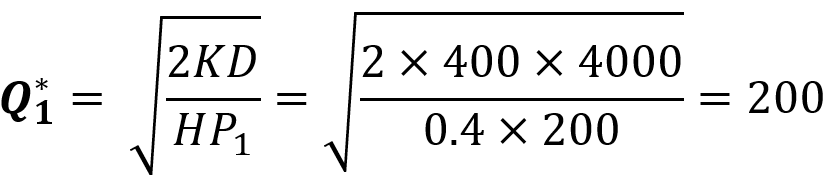
این مقدار در بازه منحنی اول قرار دارد. اگر مقدار سفارش را ۲۰۰ واحد تعیین کنیم، هزینههای موجودی برابر است با:
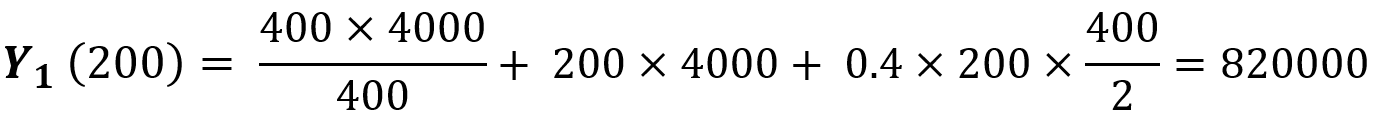
این هزینه بیشتر از وقتی است که مقدار سفارش را ۴۰۰ واحد تعیین میکنیم، بنابراین از آن جایی که قیمت دیگری برای بررسی نمانده، مقدار اقتصادی سفارش را ۴۰۰ واحد در نظر میگیریم.


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.