شما در حال خواندن درس مدل مقدار اقتصادی تولید (EPQ) از مجموعه مدیریت موجودی هستید.
در شکل ساده مدل EOQ و مدلهای دیگری که تا این لحظه بررسی کردیم، نحوه محاسبه هزینهها و دریافت سفارشات بیشتر مطابق با این فرض بود که اقلام را به طور آماده از دیگران خریداری میکنیم. اما میدانیم که همه اقلام با خریداری کردن تأمین نمیشوند، بلکه شاید خیلی از آنها را خودمان تولید کنیم. مدل EOQ علاوه بر تعیین مقدار خرید کالا، میتواند برای تعیین مقدار تولید مفید باشد. وقتی مقدار سفارش (Q) را با مدل EOQ محاسبه میکنیم:
۱- اگر کالا خریدنی باشد، مقدار Q نشان میدهد که در هر دوره باید چه تعداد از آن کالا را خریداری کنیم.
۲- اگر کالا ساختنی باشد، مقدار Q نشان میدهد که در در هر دوره باید چه تعداد از آن را تولید کنیم.
برای این که مدل ساده EOQ انطباق بیشتری با فرایندهای تولید کالا -جای فرایندهای خرید کالا- داشته باشد، مناسب است تغییراتی در آن اعمال کنیم. همانطور که در درس فرایندهای تولید گفتیم، فرایندهای متفاوتی برای تولید هر کالا وجود دارد؛ بنابراین برای تنظیم هر چه بهتر مدل EOQ باید بدانیم کالای مورد نظر با چه فرایندی تولید میشود. در این درس فرض میکنیم کالای مورد نظر با فرایند دستهای (Batch) تولید میشود. با این فرض علاوه بر تغییرات جزئی که اشاره خواهیم کرد، مناسب است دو تغییر مهم را در مدل EOQ اعمال کنیم:
۱- تابع هزینه را اصلاح کنیم. در شکل ساده مدل EOQ تابع هزینه شامل: هزینههای ثابت ثبت سفارش، هزینههای خرید و هزینههای نگهداری است. وقتی کالا را خودمان با فرایند دستهای تولید میکنیم، هزینههای خرید حذف میشوند و ضمناً دقیقتر است که «هزینههای ثابت هر نوبت تولید» که اغلب شامل هزینههای تنظیم و راهاندازی تجهیزات است را جایگزین «هزینههای ثابت ثبت سفارش» کنیم.
۲- در مدل EOQ فرض بر این بود که همه آن چه سفارش میدهیم، در یک لحظه مشخص -نقطه آغازین دوره جدید- در اختیارمان قرار میگیرد. این فرض شاید با فرایندهای خرید کالا هماهنگ باشد، اما خیلی اوقات با فرایندهای تولید کالا هماهنگ نیست. معمولاً وقتی خودمان یک کالا را تولید میکنیم، هر یک واحد از کالا که تولید میشود، از همان زمان در دسترس قرار میگیرد و میتوانیم از آن استفاده کنیم. لذا در مدل جدید فرض را بر این میگذاریم که کالاهای تولید شده به تدریج در دسترس قرار میگیرند، نه این که Q واحد از کالا ساخته شود و بعد تمام Q واحد همزمان در دسترس قرار بگیرند.
با این تغییرات و فرضهای جدیدی که اشاره خواهیم کرد به مدلی دست پیدا میکنیم که در بسیاری از منابع با عنوان مدل مقدار اقتصادی تولید (Economic Production Quantinty) یا EPQ معرفی شده است. لذا EPQ همان EOQ است، با این تفاوت که بعضی فرضهای آن تغییر کرده تا هماهنگی بیشتری با تامین موجودی از طریق تولید کالا با فرایندهای تولید دستهای داشته باشد.
۱- فرضهای مدل مقدار اقتصادی تولید (EPQ)
فرضهای جدید در مدل EPQ باعث میشوند تغییرات سطح موجودی در گذر زمان مطابق نمودار زیر باشد.
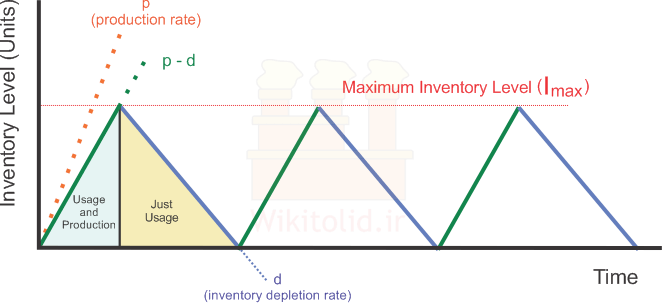
به جز مواردی که در ادامه خواهیم گفت، تمام فرضهایی که قبلاً برای مدل EOQ گفتیم در مدل EPQ نیز وجود دارند. برای درک بهتر فرضهای جدید، تلاش کنید موارد زیر را با نمودار بالا انطباق دهید.
۱- در مدل EPQ همچون مدل EOQ، یک دوره با ویژگیهای معین بارها در افق زمانی مورد نظر تکرار میشود. آغاز هر دوره مقارن با آغاز یک نوبت تولید به مقدار Q واحد کالا است. بعد از این که Q واحد کالا تولید شد، تولید متوقف میشود اما دوره ادامه مییابد تا سطح موجودی به صفر برسد.
۲- در شکل ساده مدل EOQ فرض بر این بود که تمام موجودیها در یک لحظه در دسترس قرار میگیرند. در مدل EPQ فرض میکنیم آن چه سفارش دادهایم به تدریج در دسترس قرار میگیرد، یعنی اگر مقدار تولید برابر ۱۰۰ واحد باشد، در هر لحظه مقداری از این ۱۰۰ واحد به موجودیها اضافه میشود. لذا در نمودار بالا موجودی بر خلاف نمودار EOQ در یک لحظه و در امتداد یک خط عمود افزایش نمییابد، بلکه افزایش آن تدریجی و در امتداد یک خط شیبدار است.
۳- موجودیها در تمام افق زمانی همواره و در هر لحظه با نرخ ثابت d در حال مصرف شدن هستند. مثلاً اگر نرخ مصرف برابر ۳۶۰۰ واحد کالا در ساعت باشد، هر دقیقه ۶۰ کالا و هر ثانیه یک واحد کالا مصرف خواهد شد.
۴- گفتیم شروع هر دوره مقارن با شروع تولید Q واحد محصول است. نرخ تولید کالا مقداری ثابت و برابر با p است. بر اساس نرخ تولید (p) و نرخ مصرف (d) میتوانیم مدت زمان تولید در هر دوره و همچنین زمان کل دوره را مشخص کنیم. فرض کنید مقدار تولید برابر ۱۲۰۰ واحد (Q=1200)، نرخ تولید برابر ۶۰۰ کالا در روز (p=600) و نرخ مصرف برابر ۱۲۰ کالا در روز (d=120) باشد. وقتی یک دوره آغاز میشود، دو روز طول میکشد تا ۱۲۰۰ واحد کالا تولید شود. گفتیم مصرف همیشه ادامه دارد، پس در همین دو روز ۲۴۰ کالا مصرف میشود و از مجموع ۱۲۰۰ واحد کالای تولید شده، ۹۶۰ واحد باقی میماند. در ادامه با این که تولید متوقف شده است، دوره ادامه مییابد و ۹۶۰ واحد کالا با نرخ ۱۲۰ واحد در روز مصرف میشوند. بدین ترتیب ۸ روز زمان میبرد تا موجودی به صفر برسد و دوره جدید آغاز شود.
۲- فهرست هزینههای مربوط به مقدار تولید
در مدل EOQ تلاش میکردیم مقداری برای سفارشات بیابیم که هزینههای موجودی به حداقل برسد. در مدل EPQ نیز همین هدف را دنبال میکنیم، اما علاوه بر هزینههای موجودی، هزینههای ثابت مربوط به هر نوبت تولید را نیز لحاظ میکنیم. به عبارتی تابع هزینه در مدل EPQ متشکل از هزینههای موجودی و هزینههای ثابت هر نوبت تولید است. البته معمولاً فرض بر این است که هزینههای ثابت هر نوبت تولید در فرایندهای دستهای بیشتر در ارتباط با هزینههای راهاندازی تولید و به ویژه تنظیم تجهیزات است، برای همین بسیاری از منابع جای «هزینه ثابت هر نوبت تولید» از «هزینه راهاندازی» استفاده میکنند. در ادامه بررسی میکنیم که چگونه باید هزینههای مختلف را در مدل EPQ محاسبه کنیم و تابع هزینهها را تشکیل دهیم.
هزینههای کمبود موجودی
در مدل EPQ همچون شکل ساده مدل EOQ فرض میکنیم کمبود موجودی به وجود نمیآید. در نموداری که بالاتر ارائه کردیم، هر زمان که موجودی به صفر میرسد، تولید جدید آغاز میشود و موجودیها افزایش مییابند. مفید است یادآوری کنیم که در مدل EPQ همچون مدل EOQ فرض بر این است که محصول دائماً در حال تولید شدن است؛ برای همین از همان لحظه که موجودی به صفر میرسد و تولید دسته جدید آغاز میشود، سطح موجودی مجدد با یک شیب ثابت (p-d) افزایش مییابد.
هزینههای نگهداری از موجودی
مقدار موجودیها دائماً تغییر میکند، لذا میتوانیم برای محاسبه هزینههای نگهداری از موجودی، مقدار میانگین را مبنا قرار دهیم. در مدل EPQ مانند مدل EOQ همه دورهها مشابه هستند، پس میانگین موجودی در کل افق زمانی برابر با میانگین موجودی در یک دوره است. هر دوره به دو قسمت تقسیم میشود. در قسمت اول، تولید انجام میشود و موجودی به تدریج افزایش مییابد تا Q واحد محصول تولید شود. در قسمت دوم تولید وجود ندارد و از موجودیها استفاده میشود تا مقدار آن به صفر برسد.
اگر نموداری که بالاتر ارائه کردیم را در نظر بگیریم، برای محاسبه مقدار میانگین موجودی در قسمتهای اول و دوم هر دوره باید حدأکثر مقدار موجودی را بدانیم. بدیهی است در هر دوره Q واحد کالا تولید میشود اما حداکثر موجودی به Q نمیرسد، زیرا گفتیم در بخش اول همانطور که کالا تولید میشود، بخشی از آن هم با نرخ d مورد استفاده قرار میگیرد.
برای تعیین مقدار کالای مصرف شده در بخش اول هر بازه، باید نرخ d را در مدت زمان آن بازه ضرب کنیم. فرض کنید t مدت زمان هر دوره، t1 مدت زمان مربوط به قسمت اول هر دوره و t2 مدت زمان مربوط به قسمت دوم هر دوره باشد. میدانیم در هر دوره Q واحد محصول تولید میشود، یس حاصل ضرب p در t1 برابر Q است. بر این اساس مقدار t1 به دست میآید.
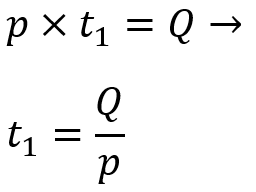
بنابراین مقدار محصولات تولید شده در قسمت اول از هر دوره برابر است با:
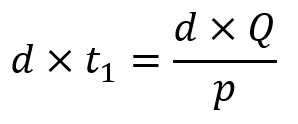
در هر دوره Q واحد محصول در قسمت اول آن دوره تولید میشود و اگر مقدار بالا را از آن کسر کنیم، حداکثر موجودی به دست میآید.
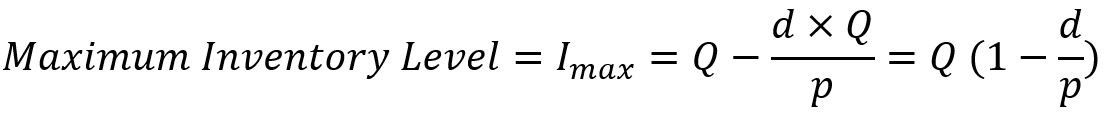
برای محاسبه میانگین موجودی، ابتدا قسمت اول هر دوره را در نظر میگیریم؛ در این بازه موجودی از صفر به Imax میرسد، پس میانگین موجودی در این بخش Imax/2 است. در بخش دوم نیز موجودی از Imax به صفر میرسد، پس در این دوره نیز میانگین موجودی Imax/2 است. بر این اساس معمولاً در مدل EPQ فرض را بر این میگذارند که میانگین مقدار موجودی سالیانه برابر Imax/2 است. البته که میدانیم لزوماً مدت بازه زمانی اول و دوم یکسان نیست و دقیقتر آن است که میانگین موجودی در هر دوره و به تبع آن در کل افق زمانی را با کمک میانگین وزندار محاسبه کنیم؛ اما برای هماهنگی مطالب با آن چه در منابع رواج یافته، فرض میکنیم میانگین مقدار موجودی برابر نصف مقدار Imax است.

در مدل EOQ برای محاسبه هزینههای نگهداری از موجودی، نرخی به اسم H داشتیم که درصدی از هزینههای خرید بود. اما در مدل EPQ چون محصولات را خریداری نمیکنیم، جای استفاده از نرخ هزینه نگهداری، مستقیماً فرض میکنیم که هزینه نگهداری از هر واحد موجودی برای کل افق زمانی -مثلاً یک سال- برابر H است. در این حالت مجموع هزینههای نگهداری از موجودی برای کل افق زمانی برابر است با:
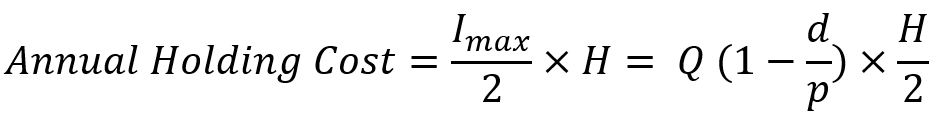
هزینههای خرید موجودی
در مدل EPQ موجودیها را خریداری نمیکنیم، بلکه خودمان میسازیم؛ پس هزینههای خرید برابر صفر است.
هزینههای راهاندازی هر نوبت تولید
گفتیم مدل EPQ در واقع برای تولید دستهای تنظیم شده است. در تولید دستهای معمولاً هزینه ثابتی که به ازای هر نوبت تولید پرداخت میکنیم در رابطه با هزینههای مربوط به تنظیم تجهیزات است. برای محاسبه تعداد نوبتهای تولید کافی است مقدار کل تقاضا در افق زمانی مورد نظر (D) را در مقدار تولید (Q) تقسیم کرده و حاصل را در هزینههای ثابت هر نوبت تولید (هزینههای راهاندازی برای هر نوبت تولید) ضرب کنیم:
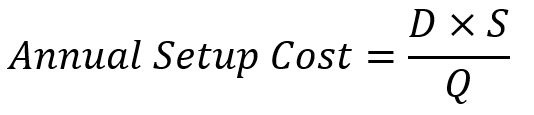
محاسبه مجموع هزینهها و تشکیل تابع هزینهها
برای تشکیل تابع هزینهها کافی است خرده هزینههایی که محاسبه کردیم را جمع کنیم:
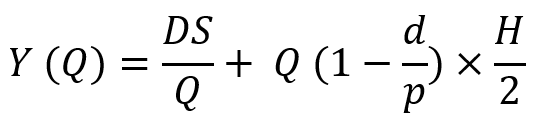
۳- تعیین مقدار بهینه برای Q
برای یافتن مقداری از Q که تابع هزینهها را به حداقل برساند، از تابع هزینهها نسبت به Q مشتق گرفته و حاصل را برابر صفر قرار میدهیم. *Q مقدار اقتصادی تولید است که به ازای آن تابع هزینه حداقل میشود.
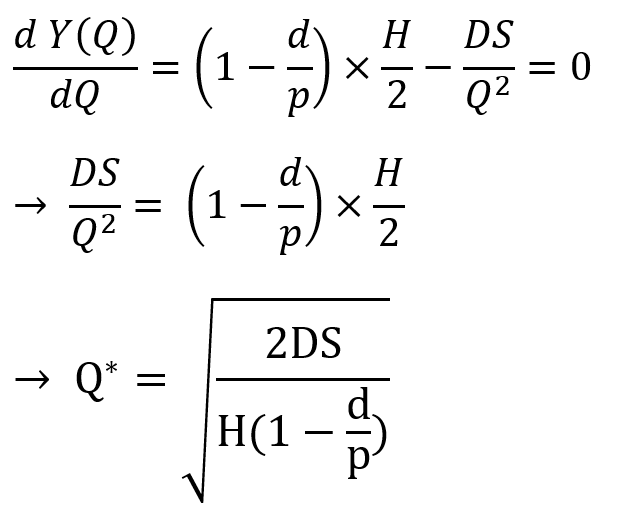
مثال
فرض کنید سالیانه ۲۰۰ روز فعالیت و هر روز به ۸ واحد از کالایی نیاز داریم. این قطعه را خودمان در دستههای ۸۰ تایی تولید میکنیم، طوری که تولید هر ۸۰ واحد از آن به ۵ روز زمان نیاز دارد. هزینه نگهداری از هر واحد برای یک سال برابر ۸ تومان و هزینه راهاندازی هر نوبت تولید برابر ۳۲ تومان است.
در این مثال نرخ مصرف روزانه ۸ واحد (d=8) و نرخ تولید روزانه ۱۶ واحد (P=16) است. با توجه به این که در هر سال ۲۰۰ روز فعالیت میکنیم و در هر روز به ۸ واحد از این قطعه نیاز داریم، تقاضای سالیانه برای این قطعه ۱۶۰۰ واحد است (D=1600). مقدار بهینه تولید در هر دوره برابر است با:
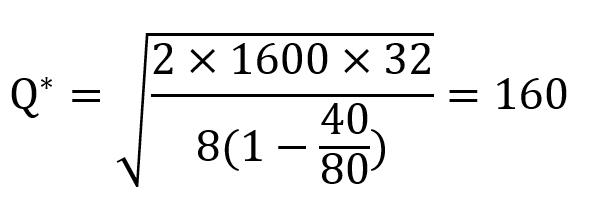


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.