مدل EOQ با فرض مجاز بودن Backordering

افزودن امکان Backordering به مدل EOQ

مدل EOQ با تکیه بر این فرض بود که کمبود موجودی نخواهیم داشت؛ برای همین می‌گفتیم: موجودی در هر دوره به صفر می‌‌رسد، اما صفر باقی نمی‌ماند، چون فوراً موجودی‌های جدید از راه می‌رسند و دوره بعدی شروع می‌شود. اما در مدل جدید می‌گوییم: هر بار که موجودی تمام می‌شود، مدتی زمان می‌برد تا موجودی‌های جدید از راه برسند. در این مدت، سطح موجودی برابر صفر باقی می‌ماند و نمی‌توانیم به تقاضای مشتریان پاسخ دهیم. یا این وجود مشتریان سفارش خود را ثبت می‌کنند و منتظر می‌مانند تا هر وقت موجودی جدید رسید، فوراً سفارش خود را دریافت کنند. سفارشی که با این شرایط ثبت می‌شود Backorder‌ نام دارد، همچنین به این شیوه پاسخ به سفارشات در شرایط کمبود موجودی Backordering می‌گویند.

در مدل جدید نیز همچون مدل EOQ می‌خواهیم مقدار اقتصادی سفارش موجودی را بیابیم، یعنی تصمیم بگیریم که موجودی‌ها را در چه مقداری سفارش دهیم تا هزینه‌های موجودی به حداقل برسد. اما علاوه بر آن باید مقدار بهینه برای تعداد سفارشاتی که به شکل Backorder ثبت می‌شوند را نیز مشخص کنیم؛ یعنی باید تصمیم بگیریم که در هر دوره به چه مقدار از تقاضا با تاخیر پاسخ دهیم.

برای پیاده‌سازی مدل جدید از همان رویه‌ای استفاده می‌کنیم که برای مدل EOQ استفاده کردیم. در بخش اول، فرض‌های جدید را توضیح می‌دهیم، طوری که کمبود موجودی مجاز باشد و در دوران کمبود موجودی از Backordering برای پاسخ به تقاضا استفاده کنیم. در بخش دوم با توجه به فرضیات جدید، هزینه‌های موجودی شامل: هزینه ثابت سفارش، هزینه خرید، هزینه نگهداری و هزینه کمبود موجودی را به زبان ریاضی توصیف کرده و آن‌ها را جمع می‌کنیم تا تابع هزینه تشکیل شود. در بخش سوم از تابع هزینه‌ها نسبت به «مقدار سفارشات موجودی» و «مقدار سفارشات Backorder» مشتق می‌گیریم تا مقادیر بهینه آن‌ها را بیابیم.

۱- فرضیات مدل EOQ با امکان تأخیر در پاسخ به تقاضا

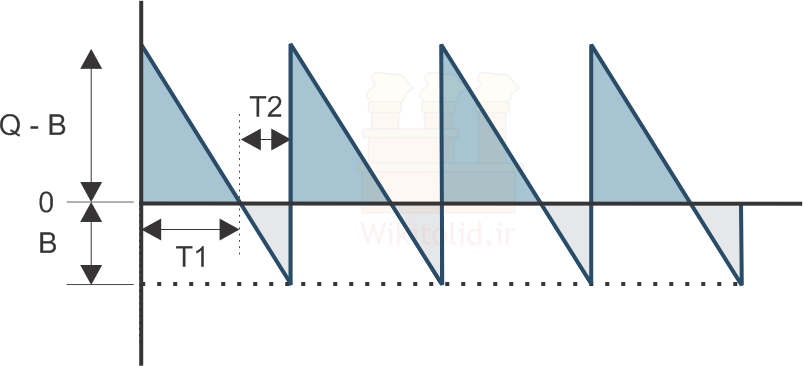
در این درس تمام فرضیات حاکم بر مدل EOQ کماکان وجود دارند، فقط فرض «مجاز نبودن کمبود موجودی» را کنار می‌گذاریم و جای آن «مجاز بودن کمبود موجودی» را مبنا قرار می‌دهیم. فرض «مجاز بودن کمبود موجودی» باعث می‌شود که مساله بسیار پیچیده‌تر شود، زیرا از یک سو مشتریان ممکن است رفتارهای متفاوتی در مواجهه با کمبود موجودی نشان دهند و از سوی دیگر عرضه‌کننده ممکن است سیاست‌های متفاوتی برای پاسخ به مشتریان داشته باشد. لذا برای ساده‌تر شدن مساله چند فرض دیگر را نیز اضافه خواهیم کرد تا دقیقاً بدانیم چه اتفاقاتی در دوره کمبود موجودی رقم خواهد خورد. با در نظر گرفتن فرض‌های حاکم بر مدل جدید، سطح موجودی مشابه نمودار زیر تغییر خواهد کرد.

برای توسعه مدل جدید، درس مدل EOQ را باز کنید و فرض‌های آن را بخوانید، سپس فرض‌ها و ملاحظات زیر را نیز به آن‌ها اضافه کنید.

۱- در این مدل نیز فرض می‌کنیم فاصله بین هر دو سفارش (T) ثابت است، مثلاً سفارشات را همیشه بعد از سه ماه ثبت می‌کنیم (T=3/12=0.25). اما همانطور که در مقدمه توضیح دادیم و در نمودار بالا می‌بینید: فاصله بین هر دو سفارش (T) شامل دو بازه متفاوت است که در بازه اول (T1): مقدار موجودی مثبت است و می‌توانیم فوراً به تقاضا پاسخ دهیم، اما در بازه دوم (T2): موجودی تمام شده و برابر صفر است، پس فقط سفارشات مشتریان را ثابت می‌کنیم تا بعداً که موجودی مثبت شد به آن‌ها پاسخ دهیم.

۲- در هر دوره (T) مقدار سفارش موجودی یا به عبارتی مقدار موجودی جدیدی که از راه می‌رسد برابر Q است. در درس مدل EOQ نیز مقدار سفارش را برابر Q فرض کرده بودیم. در هر دوره تعداد سفارشاتی که به شکل Backorder‌ هستند، یعنی سفارشاتی که ثبت می‌کنیم اما بعداً به مشتری تحویل می‌دهیم، برابر B است. هر بار که موجودی جدید از راه می‌رسد و دوره جدید شروع می‌شود، B‌ واحد از آن را بر می‌داریم تا به سفارشات مربوط به دوره قبل پاسخ دهیم. برای همین درست است که مقدار سفارشات موجودی برابر Q است و در ابتدای هر دوره Q واحد موجودی در اختیارمان قرار می‌گیرد، اما B واحد از آن فوراً بابت سفارشات قبلی از دست می‌رود و Q-B واحد از آن به عنوان موجودی ذخیره می‌شود.

۳- متقاضیان وقتی با کمبود موجودی مواجه می‌شوند، واکنش‌های متفاوتی نشان می‌دهند. برای مثال شاید: به کلی از خرید منصرف شوند، منتظر بمانند تا موجودی افزایش یابد و بعد برای خرید محصول مراجعه کنند، سفارش خود را ثبت کنند تا هر وقت محصول موجود شد به آن‌ها تحویل داده شود یا محصول مشابهی را از دیگران خریداری کنند. اما در این درس فرض می‌کنیم که: «هر گاه کمبود موجودی داریم، مشتریان سفارش خود را ثبت می‌کنند و منتظر می‌مانند تا موجودی افزایش یابد و سفارش خود را دریافت کنند».

۴- اصولاً وقتی درخواست مشتریان را با تاخیر پاسخ می‌دهیم، هزینه‌هایی بر ما تحمیل می‌شود که در حالت عادی نمی‌پردازیم. مثلاً شاید از مشتری بخواهیم که سفارش خود را با تاخیر تحویل بگیرد، اما جای آن محصول را با قیمت پایین‌تر، خدمات بیشتر یا کیفیت بالاتر خریداری کند. در این حالت امتیازاتی که به مشتری می‌دهیم، هزینه‌هایی هستند که به دلیل کمبود موجودی می‌پردازیم. همچنین این شرایط ممکن است به اعتبار برند و وفاداری مشتریان لطمه وارد کند و در بلند مدت هزینه‌هایی را به همراه داشته باشد. در این درس فرض می‌کنیم به تاخیر افتادن تحویل هر واحد موجودی به مدت یک سال، هزینه‌ای برابر J تحمیل می‌کند. لذا اگر J برابر ۱۲۰ هزار تومان باشد، تحویل هر واحد محصول با یک ماه تاخیر ۱۰ هزار تومان هزینه خواهد داشت.

۲- هزینه‌های موجودی در شرایط مجاز بودن تاخیر در پاسخ به تقاضا

در مدل EOQ و مدلی که در این درس توسعه می‌دهیم، هزینه‌های موجودی شامل چهار گروه: هزینه‌های کمبود موجودی، هزینه‌های ثابت سفارش، هزینه‌های خرید و هزینه‌های نگهداری هستند. در ادامه قصد داریم رابطه ریاضی هر کدام از هزینه‌های موجودی با «مقدار سفارشات» و «مقدار سفارشاتی که به صورت Backorder ثبت می‌شوند» را بیابیم.

گروه اول: هزینه‌های کمبود موجودی

در این مدل فرض کرده‌ایم که هر وقت یک واحد موجودی را با یک سال تاخیر به متقاضی تحویل دهیم، هزینه آن برابر J است. یعنی اگر J‌ برابر ۲۴۰ تومان باشد، هزینه اضافه بابت تحویل هر واحد موجودی با ۴ ماه تاخیر برابر ۸۰ تومان است.

سفارشاتی که قرار است با تاخیر تحویل دهیم، فقط در بخش T2 از هر دوره ثبت می‌شوند. در بخش اول هر دوره یا در بازه T1 همه سفارشات را فوراً پاسخ می‌دهیم و مقدار سفارشات Backorder صفر است. در بازه T2 تعداد موجودی‌هایی که باید بعداً تحویل دهیم در ابتدا صفر است و در پایان دوره به B می‌رسد، پس در بازه T2‌میانگین موجودی‌هایی که قرار است به شکل Backorder در دوره بعد تحویل دهیم برابر B/2 است. اما برای این که بدانیم در هر دوره T، به طور متوسط چند موجودی به شکل Backorder ثبت و با تاخیر تحویل داده می‌شود، باید از مقدار متوسط آن‌ها در بازه T1 و مقدار متوسط آن‌ها در بازه T2 میانگین بگیریم:

در این درس قصد داریم مقادیر بهینه Q و B را بیابیم، پس باید حتی‌المقدور روابط را طوری بنویسیم که مقدار آن‌ها فقط بر اساس همین متغیرها قابل تعیین باشد. مقادیر T‌ و T1 و T2 از روابط زیر به دست می‌آیند.

با قرار دادن مقادیر T1 و T2 در معادله‌ای که بالاتر نوشتیم، میانگین تعداد سفارشاتی که به عنوان Backorder در هر دوره ثبت می‌شوند را می‌توانیم با کمک رابطه زیر محاسبه کنیم.

همانطور که گفتیم هزینه تاخیر در تحویل هر واحد موجودی را به طور سالیانه برابر J در نظر می‌گیریم؛ پس برای این که بتوانیم هزینه کمبود موجودی در هر دوره را حساب کنیم، باید این مقدار را بر تعداد دوره‌ها تقسیم کنیم.

هر سال از چند دوره تشکیل می‌شود، پس برای این که بتوانیم هزینه سالیانه کمبود موجودی را محاسبه کنیم، کافی است رابطه بالا را در تعداد دوره‌ها ضرب کنیم.

گروه‌های دوم و سوم: هزینه‌های خرید و سفارش موجودی

هزینه خرید و هزینه ثابت هر نوبت سفارش موجودی ارتباطی با فرض‌های این درس ندارند، لذا مقدار آن‌ها به همان شکلی محاسبه می‌شود که در مدل EOQ محاسبه کردیم.

گروه چهارم: هزینه‌های نگهداری

معمولاً هزینه سالیانه نگهداری از هر واحد موجودی را به عنوان درصدی از هزینه‌های خرید اعلام می‌کنیم؛ در این درس نرخ هزینه‌های نگهداری را با H نشان می‌دهیم. اگر هزینه خرید هر واحد محصول برابر P باشد، هزینه نگهداری از آن برای یک سال برابر H.P خواهد بود.

برای محاسبه مجموع هزینه‌های سالیانه نگهداری، باید هزینه نگهداری از هر واحد موجودی یعنی H.P را در تعداد موجودی‌ها ضرب کنیم. با توجه به این که تعداد موجودی‌ها دائماً تغییر می‌کند، باید میانگین آن در طول یک سال را محاسبه کنیم.

در بازه T1 مقدار موجودی از Q-B شروع می‌شود و به صفر می‌رسد، پس میانگین موجودی در دوره T1 برابر نصف مقدار Q-B است. در بازه T2 موجودی و میانگین آن برابر صفر است. بنابراین میانگین موجودی در هر دوره از رابطه زیر به دست می‌آید.

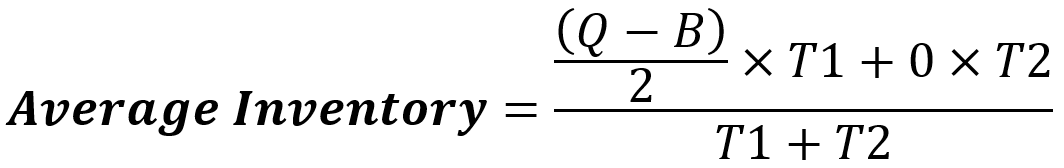
ترجیح ما این است که تمام مقادیر را بر اساس Q و B بنویسیم، ضمن این که بالاتر دیدیم مقادیر T1 و T2‌ برابر زیر هستند:

با جای گذاری T1 و T2 در معادله‌ای که بالاتر برای میانگین موجودی نوشتیم، رابطه زیر به دست می‌آید.

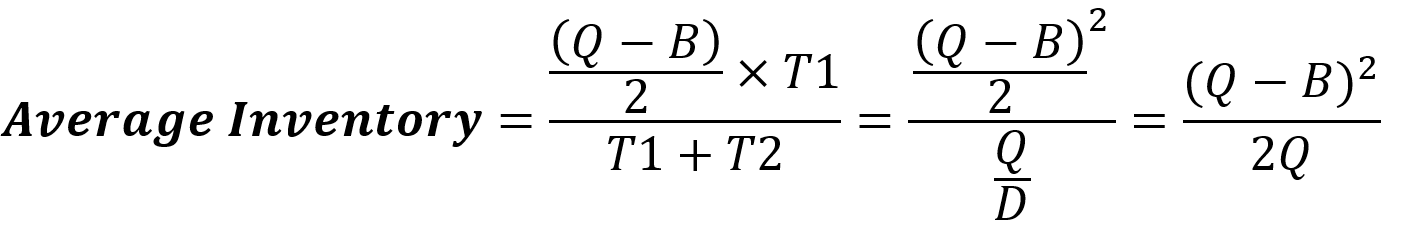
میانگین موجودی در کل سال نیز برابر با میانگین موجودی هر دوره است، لذا هزینه‌های نگهداری از موجودی را می‌توانیم با ضرب حاصل رابطه بالا در H.P محاسبه کنیم.

مجموع هزینه‌های موجودی

اگر این چهار نوع هزینه را جمع کنیم، مجموع هزینه‌های موجودی به دست می‌آید. در روابطی که برای هزینه‌ها نوشتیم، همه پارامترها مقادیر مشخص و ثابتی دارند، به جز پارامترهای Q و B که متغیر هستند. بر این اساس مجموع هزینه‌ها را به عنوان تابعی از پارامترهای Q و B تشکیل می‌دهیم.

۳- تعیین مقدار بهینه برای Q و B

برای یافتن بهینه‌ترین مقدار برای سفارشات موجودی (Q) و مقدار سفارشاتی که با تاخیر به آن‌ها پاسخ می‌دهیم (B)، ابتدا از تابع Y(Q,B) نسبت به B مشتق می‌گیریم و حاصل را برابر صفر قرار می‌دهیم. با این کار می‌توانیم ارتباط میان B و Q را پیدا کنیم.

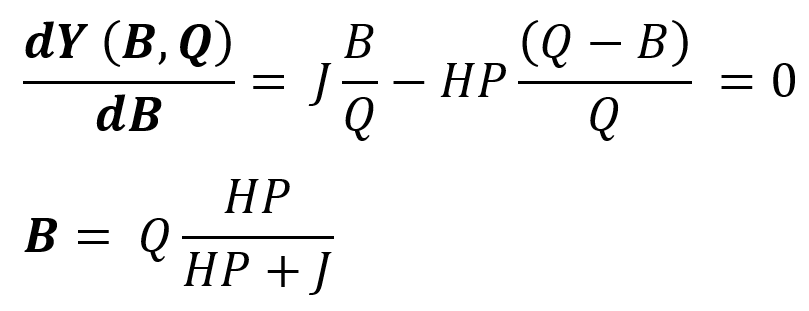
برای یافتن مقدار بهینه Q از تابع Y(B,Q) نسبت به Q مشتق می‌گیریم و آن را برابر صفر قرار می‌دهیم.

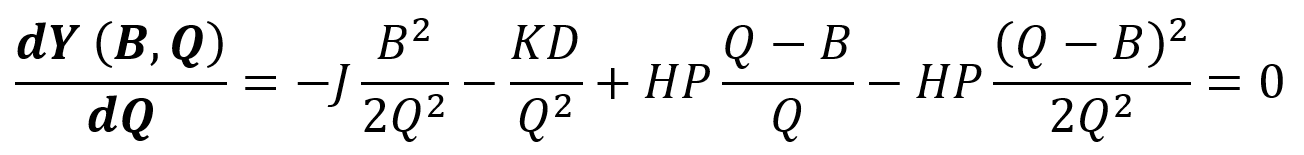
مقدار B را در رابطه بالا قرار می‌دهیم تا فقط یک متغیر داشته باشیم.

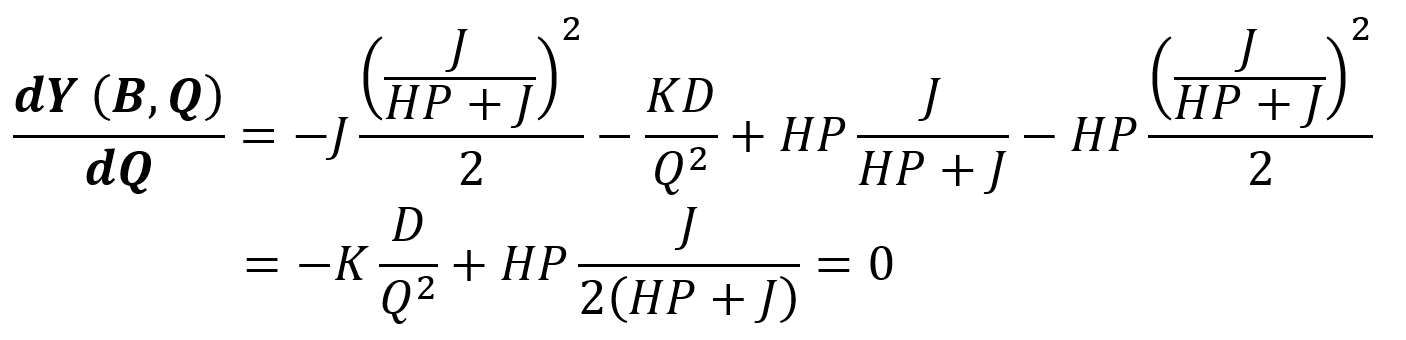
در رابطه بالا همه پارامترها به جز Q یک مقدار ثابت هستند. بنابراین می‌توانیم مقدار بهینه Q (یا *Q) را به صورت زیر حساب کنیم.

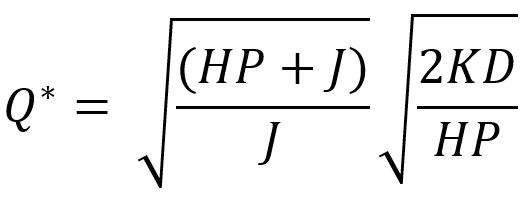
اگر مقدار *Q را در معادله‌ای که بالاتر برای B نوشتیم قرار دهیم، مقدار بهینه برای تقاضایی که ثبت می‌کنیم اما با تاخیر تحویل می‌دهیم به دست می‌آید.

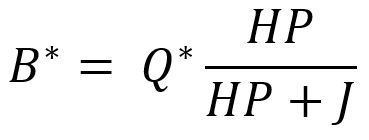
اگر به رابطه‌ای که برای *Q نوشتیم دقت کنیم، متوجه می‌شویم که بخشی از آن همان رابطه‌ای است که در مدل EOQ برای تعیین مقدار *Q استفاده می‌کنیم. در مدل ساده EOQ مقدار اقتصادی از رابطه زیر به دست می‌آید:

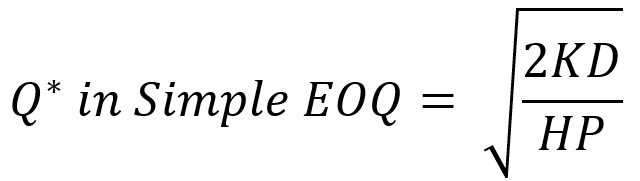
بنابراین می‌توانیم بگوییم مقدار بهینه در مدل جدید به شکل زیر است. با توجه به رابطه زیر، تعداد سفارشات در مدل جدید همیشه بیشتر از تعداد سفارشات در مدل EOQ است.

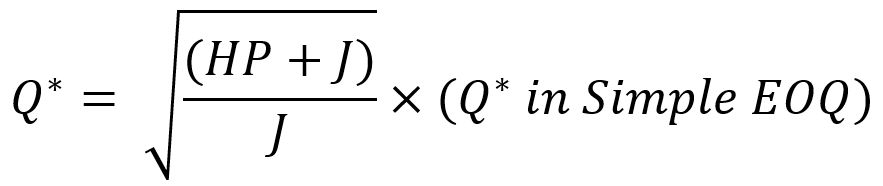
در مدل جدید، فاصله بین سفارشات از رابطه زیر به دست می‌آید:

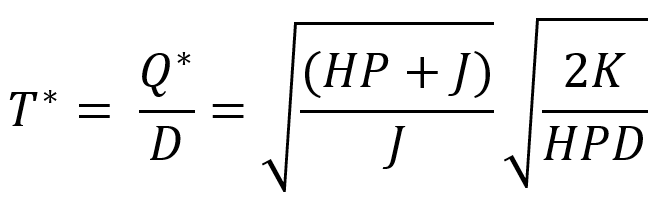
اگر از مقادیر بهینه *Q و *B استفاده کنیم، مقدار تابع Y(Q,B) به حداقل می‌رسد. لذا حداقل مقدار هزینه‌های موجودی در شرایطی که Backordering مجاز است با رابطه زیر به دست می‌آید.

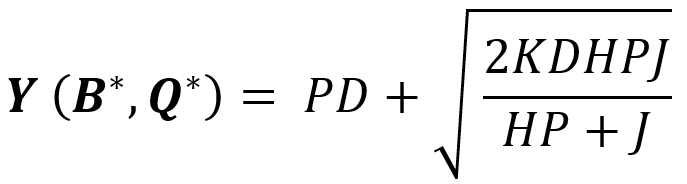
مثالی برای EOQ با فرض مجاز بودن Backordering

در درس مدل EOQ مثالی زدیم که در آن تقاضای سالیانه برای موجودی ۷۲۰ واحد (D=720)، هزینه ثابت سفارش برای هر موجودی برابر ۲۰ تومان (K=20)، هزینه خرید هر واحد محصول برابر۲۰ تومان (P=20) و هزینه نگهداری از هر واحد محصول سالیانه ۱۰% قیمت خرید (H=0.1) بود. در آن مثال مقدار اقتصادی سفارش (*Q) را ۱۲۰ واحد و هزینه بهینه را ۱۴۶۴۰ تومان محاسبه کردیم. اکنون فرض می‌کنیم که کمبود موجودی مجاز است و تاخیر در تحویل هر واحد موجودی ۵ تومان هزینه دارد (J=5). با این فرض مقدار بهینه سفارش (*Q) را از رابطه زیر به دست می‌آوریم:

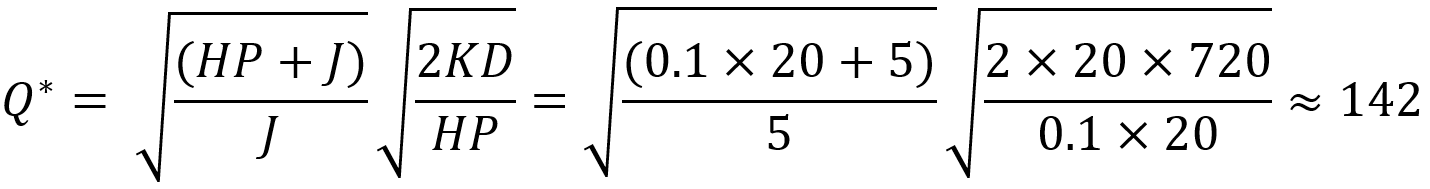
مقدار موجودی که در هر دوره توسط مشتریان تقاضا می‌شود، اما تحویل آن را به دوره بعد موکول می‌کنیم برابر است با:

اگر مقدار سفارشات در هر دوره را ۱۴۲ واحد و مقدار تقاضایی که با تاخیر پاسخ می‌دهیم را ۴۱ واحد انتخاب کنیم، مجموع هزینه‌ها برابر است با:

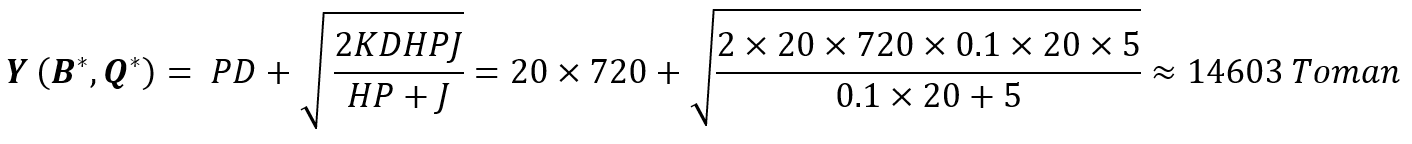
پس با مجاز کردن Backorder اولاً مقدار سفارشات در هر دوره از ۱۲۰ واحد به ۱۴۲ واحد می‌رسد و ثانیاً مجموع هزینه‌ها از ۱۴۶۴۰ تومان به ۱۴۶۰۳ تومان کاهش می‌یابد. به طور کلی هر چه J کم‌تر باشد، سیاست به تاخیر انداختن پاسخ به تقاضا موثرتر خواهد بود. مثلاً فرض کنید J برابر ۲ باشد؛ در این حالت مقدار *B به ۸۵ واحد می‌رسد و مجموع هزینه‌ها به ۱۴۵۷۰ تومان کاهش می‌یابد. اما اگر J برابر ۲۰ باشد، مقدار اقتصادی *B به ۱۱ واحد کاهش و مجموع هزینه‌ها به ۱۴۶۲۹ تومان افزایش می‌یابد؛ در این حالت Backordering تاثیر چندانی در کاهش هزینه‌های موجودی ندارد، لذا می‌بینیم مقدار *B بسیار کم‌تر از حالت‌های دیگر محاسبه می‌شود.