شما در حال خواندن درس مدل مقدار اقتصادی سفارش (EOQ) از مجموعه مدیریت موجودی هستید.
در مدیریت موجودی، بخشی از مهمترین مسائلی که با آنها روبهرو میشویم و تصمیمهایی که اتخاذ میکنیم در ارتباط با تعیین «مقدار سفارشات» و «زمانبندی سفارشات» هستند.
در موضوع این درس، منظور از سفارش این است که درخواست مربوط به خرید یا ساخت یک کالا را ثبت کنیم تا آن کالا در موعد مورد نظر در دسترس قرار بگیرد و موجودی آن افزایش یابد. مثلاً فرض کنید یکی از موجودیها، نوعی سیلندر است که خودمان آن را میسازیم. در این حالت سفارش یعنی به کارگاه بسپاریم که مقداری از این کالا را بسازد. همچنین ممکن است یکی دیگر از موجودیها نوعی پیچ باشد که آن را به طور آماده از بازار خریداری میکنیم. در این حالت سفارش یعنی تشریفات خرید آن پیچ از تامینکننده را انجام دهیم تا کالای مورد نظر در موعد مقرر در دسترس قرار بگیرد.
فرض کنید کارگاه برای ساخت ۲۰ واحد سیلندر به دو هفته زمان نیاز داشته باشد. با این فرض که موجودی این قطعه یک ماه دیگر تمام میشود، تصمیم میگیریم که سفارش ساخت را دو هفته دیگر ثبت کنیم. در این حالت مقدار سفارش برابر ۲۰ واحد و زمان سفارش دو هفته دیگر است.
مدل مقدار سفارش اقتصادی یا Economic Order Quantity یا به اختصار EOQ ابزاری برای تعیین مقدار و زمانبندی سفارشات است که در سال ۱۹۱۳ توسط فورد ویتمن هریس ارائه شد.
تفکر حاکم بر مدل EOQ بسیار ساده و منطقی است: «مقدار سفارش را طوری تعیین کنیم که مجموع هزینههای موجودی به حداقل برسد». قاعدتاً خیلی از مدلهای دیگر نیز در صدد کاهش هزینههای موجودی هستند و بدین لحاظ میتوانیم آنها را در چهارچوب مدل EOQ تصور کنیم. اما تفاوت اساسی این مدلها در میزان سادهسازی است؛ مدل EOQ برای سادهسازی مساله و محاسبه هزینههای موجودی، فرضهای زیادی را در نظر میگیرد که بسیاری از آنها با واقعیت انطباق ندارند. اما نسخههای پیشرفتهتر این مدل با تغییر در فرضها، مساله را طوری تعریف میکنند که به واقعیت نزدیکتر باشد. مثلاً مدل ساده EOQ فرض میکند که کمبود موجودی هرگز اتفاق نمیافتد، اما مدلهایی داریم که این محدودیت را ندارند و هزینههای کمبود موجودی را نیز در نظر میگیرند.
در این درس، سادهترین نسخه مدل EOQ را ارائه خواهیم کرد. فرضهای زیاد این مدل سبب میشوند که گزینه مناسبی برای بسیاری از مسائل کنترل موجودی نباشد، با این وجود خیلی از مدلهای پیشرفتهتر بر اساس همین مدل بنا شدهاند؛ لذا برای یادگیری آنها در درسهای آینده باید ابتدا با مدل EOQ آشنا شویم.
توسعه مدل EOQ به شکل ساده
در ادامه قصد داریم که نسخه سادهای از مدل EOQ را توسعه دهیم. بدین منظور:
۱- ابتدا با فرضیات مدل EOQ آشنا خواهیم شد؛ این فرضیات چهارچوب مساله را تعریف میکنند. اگر این چهارچوب با شرایط واقعی منطبق باشد، مدل EOQ گزینه مطلوبی برای یافتن مقدار سفارش است. اما در غیر این صورت باید از مدلهایی استفاده کنیم که فرضهای حاکم بر آنها، انطباق بیشتری با واقعیتهای موجودی داشته باشد.
۲- در بخش دوم، انواع هزینههای موجودی شامل: هزینه ثابت سفارش، هزینه خرید، هزینه نگهداری و هزینه کمبود موجودی را به زبان ریاضی مینویسیم. هدف از مدل EOQ این است که مجموع این هزینهها را به حداقل برسانیم، پس نهایتاً این هزینهها را جمع میکنیم و تابع هزینهها را تشکیل میدهیم.
۳- در بخش سوم تلاش میکنیم مقداری برای سفارش بیابیم که باعث شود مقدار تابع هزینههای موجودی به حداقل برسد.
۴- در بخش چهارم بر اساس مقدار سفارش (نتیجه بخش قبل)، فاصله بین سفارشات و سطح سفارش مجدد را محاسبه میکنیم. فاصله بین سفارشات، مدت زمان بین هر دو سفارش را نشان میدهد. سطح سفارش مجدد (Reorder Level) عددی است که هر وقت مقدار موجودی به آن میرسد، باید سفارش بعدی را ثبت کنیم.
۱- فرضیات مدل EOQ
گفتیم که شکل سادهی مدل EOQ از فرضیات زیادی استفاده میکند و محدودیتهای زیادی دارد. نمودار زیر بر اساس فرضیات مدل EOQ ترسیم شده است و نشان میدهد که اگر آنها را مبنا قرار دهیم، تغییرات موجودی در گذر زمان به چه شکل خواهد بود.
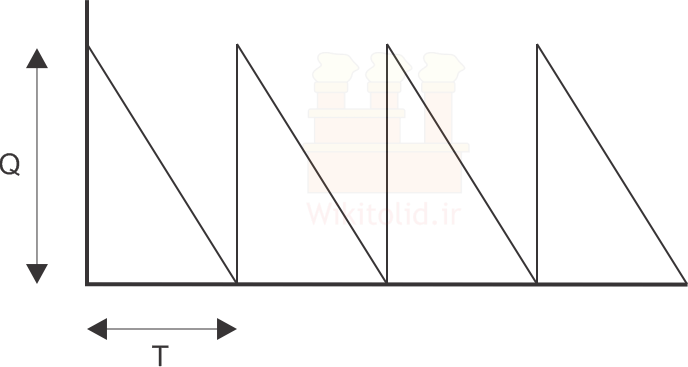
در ادامه مهمترین محدودیتها و فرضهای مدل EOQ را توضیح خواهیم داد. البته همانطور که گفتیم نسخههای پیشرفتهتری از مدل EOQ نیز وجود دارد که از فرضهای دیگری پیروی میکنند. فرضهای زیر مربوط به شکل ساده مدل EOQ هستند.
۱- این مدل برای تعیین مقدار سفارش یک نوع موجودی کاربرد دارد؛ پس اگر چند کالای مختلف داشته باشیم، برای استفاده از این مدل باید مقدار مناسب برای سفارش هر کالا را جداگانه محاسبه کنیم.
۲- در این مدل فرض بر این است که میتوانیم در افق زمانی مورد نظر، مقدار تقاضا برای موجودی را با دقت مناسبی پیشبینی کنیم. در این درس منظور از تقاضا، مقدار موجودی مورد نیاز است که شاید از درون یا بیرون سازمان نشات گرفته باشد. مثلاً شاید ماهیانه ۲۰ واحد از یک موجودی را برای مصارف داخل سازمان و ۸۰ واحد از آن را برای عرضه به بازار نیاز داشته باشیم، در این حالت میگوییم تقاضا برای آن کالا ماهیانه ۱۰۰ واحد است.
۳- فرض میکنیم همیشه میتوانیم به تقاضا پاسخ دهیم و طوری برنامهریزی کنیم که با کمبود موجودی مواجه نشویم؛ لذا در شکل ساده مدل EOQ هزینه کمبود موجودی همیشه برابر صفر است.
۴- فرض میکنیم موجودیها همواره در حال مصرف شدن هستند. همانطور که در نمودار بالا میبینیم، مقدار موجودی در راستای یک خط صاف کاهش مییابد. اگر این فرض وجود نداشت، مقدار موجودی به صورت پلهای کاهش پیدا میکرد. فرض مصرف دائم موجودیها به ندرت با واقعیت منطبق است، اما معمولاً تأثیر قابل توجهی بر دقت نتایج ندارد و خیلی از مدلهای پیشرفته نیز از این فرض پیروی میکنند. البته اگر فاصله میان نوبتهای استفاده از موجودیها و مقدار مصرف موجودیها در هر نوبت زیاد باشد، این فرض میتواند به طور قابل توجهی از دقت محاسبات بکاهد.
۵- فرض میکنیم نرخ تقاضا برای موجودی همواره ثابت میماند. مثلاً اگر کارخانه در یک سال به ۱۲۰ واحد موجودی نیاز دارد، هر ماه ۱۲ واحد موجودی مصرف میکند، نه این که مصرف آن در یک ماه به ۸ واحد و ماه دیگر به ۱۶ واحد برسد. بدون این فرض، روند تغییر موجودیها در نمودار بالا به جای یک خط صاف به منحنی تبدیل میشد.
۶- فرض میکنیم دقیقاً همان موقع که موجودی تمام میشود، سفارشی که آخرین بار ثبت کردهایم در دسترس قرار میگیرد و به واسطه آن مقدار موجودی افزایش مییابد. این فرض یک محدودیت مهم است، زیرا خیلی اوقات ترجیح میدهیم کالای سفارش داده شده را زودتر از پایان یافتن موجودی دریافت کنیم تا ریسک کمبود موجودی کاهش یابد. اما مدل EOQ نگاه ایدهآلی به شرایط دارد و فرض میکند سفارشات همیشه به موقع میرسند و کمبود موجودی اتفاق نمیافتد.
۷- فرض میکنیم سفارشات به طور آنی تحویل داده میشوند و همان لحظه که به ما تحویل داده شدند مقدار موجودی افزایش مییابد. بر اساس همین فرض در نمودار بالا میبینیم که دقیقاً در همان نقاطی که موجودی به صفر رسیده، سفارشات جدید در دسترس قرار گرفتهاند و مقدار موجودی به طور ناگهانی افزایش یافته است.
۸- فرض میکنیم که در افق زمانی مورد نظر تمام پارامترهای موثر در مدل EOQ مثل: انواع مختلف هزینهها، مقدار تقاضا، نرخ مصرف موجودی و مدت زمان مورد نیاز برای تحویل سفارش ثابت میمانند.
۲- تعیین هزینههای موجودی
در EOQ برای تعیین مقدار اقتصادی سفارش تلاش میکنیم که مجموع هزینههای موجودی را به حداقل برسانیم؛ پس قبل از هر چیز باید بتوانیم هزینههای موجودی را به زبان ریاضی توصیف کنیم. در درس هزینه موجودی سه گروه از هزینهها را اعلام کردیم که شامل: هزینههای کمبود موجودی، هزینههای خرید و هزینههای نگهداری بودند. در مدل EOQ، بخشی از مواردی که به عنوان هزینههای خرید منظور کرده بودیم از این گروه خارج میشوند و در گروه جدیدی با عنوان «هزینههای ثابت سفارش» جای میگیرند. بدین ترتیب در مدل EOQ هزینههای موجودی به چهار گروه: هزینههای کمبود موجودی، هزینههای ثابت سفارش، هزینههای خرید و هزینههای نگهداری، تقسیم میشوند. در ادامه هر کدام از این هزینهها را به زبان ریاضی توصیف خواهیم کرد. بدین ترتیب با جمع کردن مجموع هزینههای این چهار گروه میتوانیم کل هزینههای موجودی را به دست بیاوریم.
گروه اول: هزینههای کمبود موجودی
در شکل ساده EOQ فرض میکنیم که هرگز با کمبود موجودی مواجه نخواهیم شد، پس هزینههای کمبود را برابر صفر در نظر میگیریم.
گروه دوم: هزینههای ثابت مربوط به ثبت سفارش
هر بار سفارشی را ثبت میکنیم، مجموعهای از هزینههای ثابت تحمیل میشود که ارتباطی با مقدار سفارش ندارند. در درس هزینه موجودی، این هزینهها را نیز بخشی از هزینههای خرید قلمداد کرده بودیم، اما در این درس آنها را تفکیک میکنیم. لازم به تأکید است که اگر هزینهای تابع مقدار سفارش باشد، از این گروه خارج میشود و حسب مورد در گروه هزینههای خرید یا هزینههای نگهداری قرار میگیرد. مثلاً تصور کنید هر بار سفارشی را ثبت میکنیم، یک نمونه از محصول را برای کنترل کیفیت به آزمایشگاه ارسال میکنیم و ۲ میلیون تومان به آزمایشگاه میپردازیم. این مبلغ ارتباطی با مقدار سفارش ندارد، مثلاً شاید مقدار سفارش ۱۰۰ واحد یا ۱۰۰۰ واحد محصول باشد، اما در هر حال فقط یک نمونه از آن را به آزمایشگاه ارسال میکنیم و هزینه این اقدام در هر نوبت سفارش دو میلیون تومان است. اما هزینههای حملونقل معمولاً بر اساس مقدار سفارش تعیین میشوند که در این صورت نباید آنها را جزء هزینههای ثابت حساب کنیم.
در این درس فرض میکنیم که با هر نوبت سفارش، هزینه ثابتی برابر K تحمیل خواهد شد. لذا برای محاسبه مجموع هزینههای ثابت ناشی از ثبت سفارش کافی است که مقدار K را در تعداد سفارشات ضرب کنیم. اما تعداد سفارشات در افق زمانی مورد نظر چقدر است؟ گفتیم که در مدل EOQ مقدار تقاضا را میدانیم. فرض کنید مقدار تقاضای سالیانه برابر D واحد باشد. فرض دیگر این بود که مقدار سفارشات همیشه یک مقدار ثابت است، در این درس مقدار ثابت سفارش را برابر Q در نظر میگیریم. با توجه به این که مجموع سفارشات ما باید برابر D باشد و مقدار هر سفارش برابر Q است، برای محاسبه تعداد نوبتهای سفارش باید D را بر Q تقسیم کنیم. بدین ترتیب مجموع هزینههای ثابت ناشی از سفارشات در افق زمانی مورد نظر را میتوانیم از رابطه زیر محاسبه کنیم.
![]()
گروه سوم: هزینههای خرید
هزینههای خرید شامل کلیه هزینههایی مثل بهای محصول، حملونقل، بیمه و امثالهم است که تابع مقدار سفارش باشند. در درس هزینه موجودی به فهرست کاملی از هزینههای خرید اشاره کردیم. از بین هزینههای اشاره شده در آن فهرست، هزینههایی که ارتباطی با مقدار سفارش ندارند و در هر نوبت سفارش باید پرداخت شوند را در گروه قبلی و سایر هزینهها را در این گروه قرار میدهیم. در این درس هزینه خرید هر واحد محصول را با P نشان میدهیم. برای محاسبه مجموع هزینه خرید کافی است P را در تعداد محصولاتی که قرار است خریداری یا ساخته شوند ضرب کنیم. همانطور که گفتیم تقاضای سالیانه را با D نشان میدهیم. مجموع هزینههای خرید در افق زمانی مورد نظر برابر است با:
![]()
گروه چهارم: هزینههای نگهداری
هزینههای نگهداری شامل مواردی مثل: هزینه سرمایه، هزینه فضای نگهداری، هزینه ناشی از خسارات و سایر مواردی هستند که در درس هزینه موجودی اشاره کردیم. در این درس هزینه نگهداری از هر واحد موجودی برای یک سال را به شکل درصدی از هزینههای خرید آن کالا نشان میدهیم. مثلاً میگوییم نرخ هزینه نگهداری هر واحد موجودی ۱۰% است، یعنی اگر هزینه خرید هر واحد موجود ۱۶۰ تومان باشد، هزینه نگهداری آن برای یک سال برابر ۱۶ تومان خواهد بود.
در این درس نرخ هزینه نگهداری را با H نشان میدهیم، بنابراین هزینه سالیانه نگهداری از هر واحد موجودی را با ضرب H در P به دست میآوریم. همچنین اگر این مقدار را در تعداد موجودیها ضرب کنیم، هزینه سالیانه نگهداری از کل موجودیها به دست میآید. اما تعداد موجودیها چقدر است؟ همانطور که بالاتر در نمودار مشاهده کردیم، مقدار موجودیها دائم تغییر میکند. در هر دوره، یعنی از زمانی که موجودیها شارژ میشوند تا وقتی که موجودیها به پایان میرسند، میانگین موجودی برابر Q/2 است. همچنین با توجه به این که نرخ مصرف موجودیها و مقدار سفارشها همواره ثابت میماند، میانگین موجودی در کل افق زمانی نیز برابر Q/2 است. لذا میتوانیم هزینه نگهداری از موجودیها در افق زمانی مورد نظر را با رابطه زیر محاسبه کنیم.
![]()
مجموع هزینههای موجودی
با جمع کردن هزینههایی که اشاره کردیم، مجموع هزینههای موجودی به دست میآید. در رابطه زیر (Q)Y تابع هزینه بر اساس مقدار سفارش (Q) است. هر گاه مقدار سفارش را جای Q قرار دهیم، مجموع هزینه موجودی به دست میآید. همانطور که در توضیحات اشاره کردیم، حرف D مقدار موجودی مورد نیاز (یا مقدار تقاضا برای موجودی)، K هزینههای ثابت در هر نوبت ثبت سفارش، P هزینه خرید هر واحد موجودی و H نرخ هزینه نگهداری از هر واحد موجودی به مدت یک سال نسبت به قیمت خرید آن است.
![]()
۳- تعیین مقدار اقتصادی سفارش (*Q)
برای محاسبه مقدار بهینه سفارش (*Q) کافی است از تابع موجودی (Q)Y نسبت به Q مشتق بگیریم و آن را برابر صفر قرار دهیم.
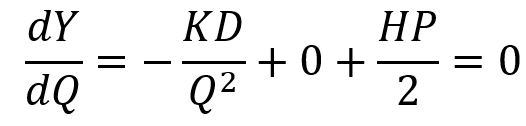
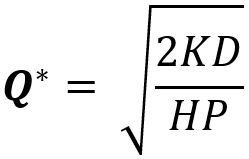
*Q مقدار اقتصادی سفارش است، پس اگر آن را در تابع هزینهها جای Q قرار دهیم، کمترین مقدار هزینه به دست میآید. مقدار بهینه هزینههای موجودی از رابطه زیر به دست میآید.
![]()
۴- تعیین فاصله زمانی بین سفارشات و سطح سفارش مجدد
در مدل EOQ فرض میکنیم که مقدار همه سفارشها برابر است، لذا به دلیل فرض دیگر مبنی بر ثابت بودن نرخ استفاده از موجودیها، فاصله بین سفارشات (T) نیز همواره یک مقدار ثابت خواهد بود. برای محاسبه فاصله بین سفارشات (*T) در حالتی که مقدار سفارشات برابر *Q است، باید مقدار اقتصادی سفارش را بر مقدار موجودی مورد نیاز تقسیم کنیم. مثلاً اگر سالیانه به ۱۰۰ واحد موجودی نیاز داشته باشیم (D=100) و مقدار اقتصادی سفارش برابر ۵۰ واحد به دست آمده باشد (۵۰=*Q)، فاصله بین سفارشات برابر با ۰٫۵ سال یا ۶ ماه است. به تعبیری میتوان گفت اگر بخواهیم هزینههای موجودی به حداقل برسد، سفارشات را باید هر ۶ ماه ثبت کنیم، پس فاصله بهینه سفارشها (*T) برابر ۰٫۵ است.
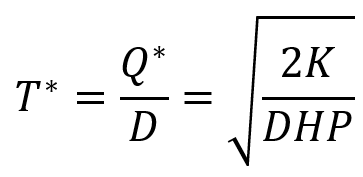
سطح سفارش مجدد (Reoder Level) مقداری است که هر موقع مقدار موجودی به آن میرسد، باید سفارش جدید را ثبت کنیم. مثلاً اگر این مقدار برابر ۲۰ واحد باشد، هر بار که موجودی به ۲۰ واحد رسید، سفارش جدید را ثبت میکنیم. برای محاسبه سطح سفارش مجدد باید مدت زمان لازم برای تحویل سفارش، یا اصطلاحاً لیدتایم سفارش، را لحاظ کنیم. اگر از زمانی که سفارش را ثبت میکنیم تا زمانی که سفارشات در دسترس قرار میگیرند ۲۰ روز فاصله باشد، میگوییم لیدتایم برابر ۲۰ روز است.
اگر لیدتایم (L) کمتر یا مساوی با فاصله بین دو سفارش (T) باشد، سطح سفارش مجدد بهینه (*R) را با ضرب تقاضای سالیانه در لیدتایم به دست میآوریم.
![]()
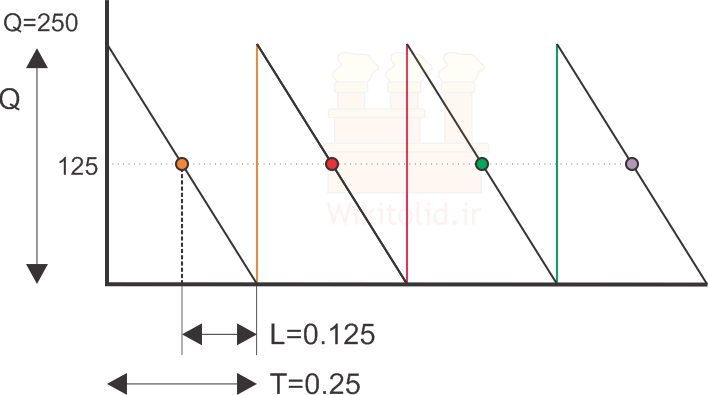
مثلاً فرض کنید سالیانه به ۱۰۰۰ واحد موجودی نیاز داریم (D=1000) و مقدار اقتصادی سفارش برابر ۲۵۰ واحد است (Q*=250)، در این حالت سالیانه باید چهار سفارش ثبت کنیم و فاصله هر دو سفارش (*T) برابر ۰٫۲۵ سال یا سه ماه به دست میآید. فرض کنید فاصله ثبت سفارش تا تحویل سفارش برابر ۰٫۱۲۵ سال با ۱٫۵ ماه باشد (L=0.125). برای محاسبه سطح سفارش مجدد باید تقاضای سالیانه (D=1000) را در لیدتایم (L=0.125) ضرب کنیم. بدین ترتیب سطح بهینه برای سفارش مجدد (*R) برابر ۱۲۵ به دست میآید، یعنی هر وقت موجودی به ۱۲۵ واحد میرسد باید سفارش جدید را ثبت کنیم.
اگر لیدتایم بیشتر از فاصله بین دو سفارش (T) باشد، سطح بهینه سفارش مجدد (*R) از رابطه زیر به دست میآید.
![]()
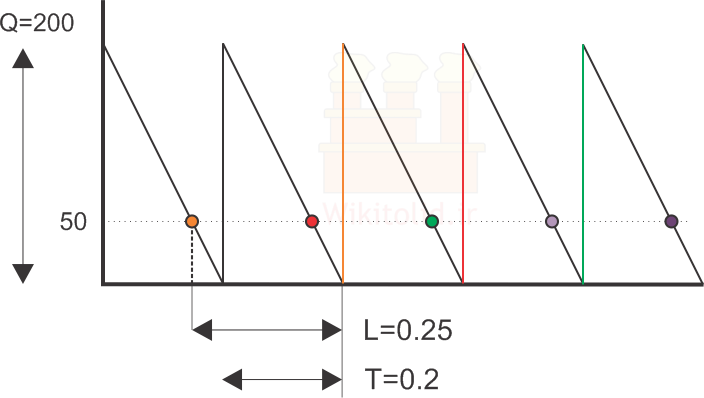
در این رابطه m باید حتماً یک عدد صحیح باشد. فرض کنید تقاضای سالیانه (D) برابر ۱۰۰۰ واحد، لیدتایم برابر ۰٫۲۵ سال و فاصله بین دو سفارش برابر ۰٫۲ سال است. در این حالت اگر m را برابر یک قرار دهیم، سطح سفارش مجدد برابر ۵۰ واحد به دست میآید. در تصویر زیر میبینیم که سفارش نارنجی ۳ ماه بعد تحویل داده شده و موجودی را افزایش داده است. خط نارنجی افزایش موجودی به واسطه این سفارش را نشان میدهد.
مثالی از مدل EOQ
کارخانهای داریم که تقاضا برای محصولات آن زیاد است و تمام محصولات آن به فروش میرود؛ بدین جهت علاقمندیم که از تمام ظرفیت کارخانه استفاده کنیم و مقدار تولید را به حداکثر برسانیم. برآوردهای ما نشان میدهد که کارخانه میتواند ظرف یک سال آینده حدود ۳۶۰ واحد محصول تولید کند. برای ساخت هر واحد محصول به دو عدد موتور نیاز است که آنها را سوای از مواد دیگر، به طور جداگانه از یک شرکت آلمانی خریداری میکنیم.
برای ثبت سفارش این محصول با یک شرکت بازرگانی قرارداد بستهایم؛ این شرکت هر بار که محصول را به درخواست ما سفارش میدهد، فارغ از این که مقدار سفارش چقدر باشد، کارمزدی برابر ۲۰ تومان دریافت میکند. همچنین از زمان ثبت سفارش، یک و نیم ماه (۰٫۱۲۵ سال) زمان لازم است تا سفارش در دسترس قرار بگیرد.
هزینه خرید هر واحد موتور با احتساب قیمت محصول، هزینههای حملونقل، مالیات، بیمه و امثالهم برابر ۲۰ تومان و هزینه سالیانه نگهداری از هر واحد موتور برابر ۱۰% هزینههای خرید آن است.
در ادامه قصد داریم که مقدار بهینه سفارش، فاصله بین سفارشها و سطح سفارش مجدد را با استفاده مدل EOQ محاسبه کنیم.
برای محاسبه مقدار اقتصادی سفارش داریم:
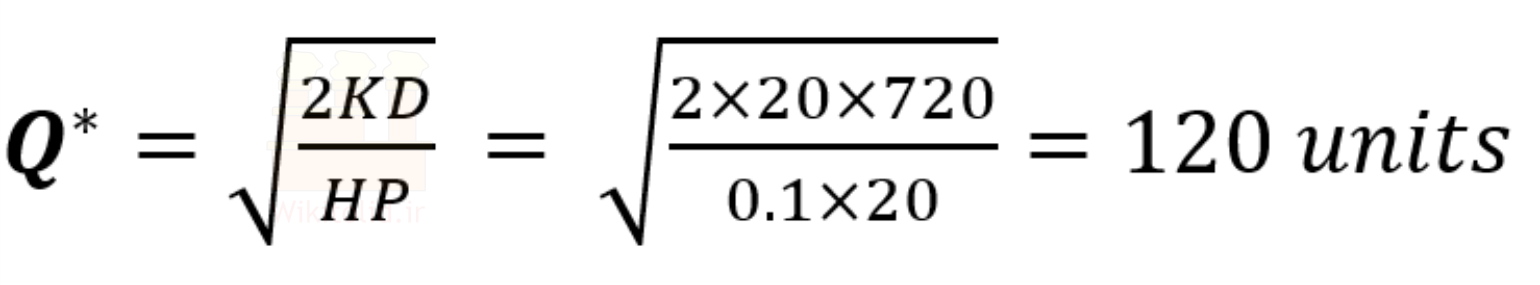
بر اساس مقداری که برای سفارش به دست آوردیم، هزینه بهینه برابر است با:
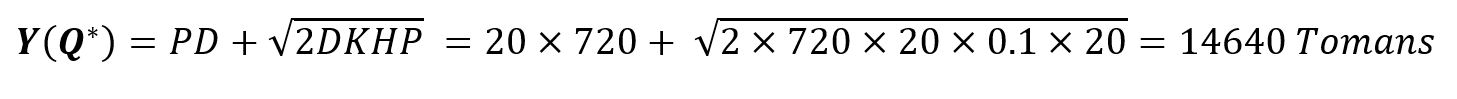
فاصله بین سفارشات و سطح سفارش مجدد برابر است با:
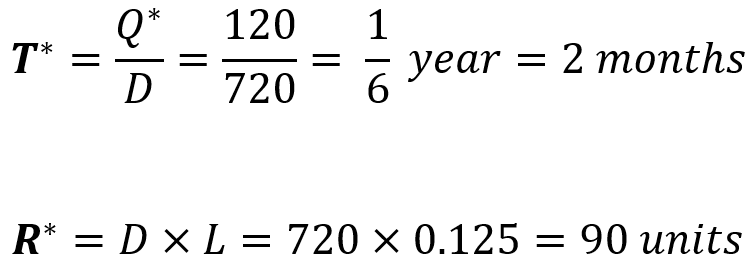


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.